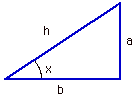
 This page is about the trigonometric functions of sine, cosine and tangent,
what they are and how to find the exact values of many angles.
This page is about the trigonometric functions of sine, cosine and tangent,
what they are and how to find the exact values of many angles.
| a | cos(a) sin(b) |
tan(a) cot(b) |
b | ||
|---|---|---|---|---|---|
| radians | ° | ° | radians | ||
| 0 | 0 | 1 | 0 | 90 | π 2 |
| π 24 |
7.5 | `color{blue}{(sqrt(2+sqrt(2+sqrt 3)))/2}` | `color{blue}{sqrt 6 - sqrt 3 + sqrt 2 - 2}` `color{blue}{= (sqrt 2 - 1)(sqrt 3 - sqrt 2)}` |
82.5 | 11 π 24 |
| π 12 |
15 |
`color{blue}{(sqrt 6 + sqrt 2)/4 = sqrt(1/2+(sqrt 3)/4) = sqrt((4+ sqrt 12)/8)}` |
`color{blue}{2-sqrt 3}` |
75 | 5 π 12 |
| cos2(15°)=[0;1,13, 1,12] | tan(15°) = [0; 3, 1, 2 ] tan2(15°) = [0; 13, 1, 12] | ||||
| π 10 |
18 |
`color{blue}{sqrt(10+2 sqrt 5)/4 = sqrt((5+sqrt 5)/8)}` |
`color{blue}{sqrt(1- (2 sqrt 5)/5)}` | 72 | 2 π 5 |
| cos2(18°) = [0; 1, 9, 2, 8] | tan2(18°) = [0; 9, 2,8] | ||||
| π 8 |
22.5 | `color{blue}{(sqrt(2+sqrt 2))/2 = sqrt((4+sqrt 8)/8)}` | `color{blue}{sqrt 2 - 1}` | 67.5 | 3 π 8 |
| cos2(22.5°) = [0; 1, 5, 1, 4] |
tan(22.5°) = [0; 2] tan2(22.5°) = [0; 5, 1, 4] | ||||
| π 6 |
30 | `color{blue}{ (sqrt 3)/2}` | `color{blue}{(sqrt 3)/3}` | 60 | π 3 |
|
cos(30°) = [ 0; 1, 6, 2, 6 ] cos2(30°) = [0; 1, 3] |
tan(30°) = [ 0; 1, 1, 2 ] tan2(30°) = [0; 3 ] | ||||
| π 5 |
36 | `color{blue}{(sqrt 5 + 1)/4 = sqrt((3+sqrt 5)/8)}` | `color{blue}{sqrt(5 - 2 sqrt 5)}` | 54 | 3 π 10 |
|
cos(36°) = [ 0; 1, 4 ] cos2(36°) = [ 0; 1, 1, 1, 8, 2 ] | tan2(36°) = [ 0; 1, 1, 8, 2 ] | ||||
| 5 π 24 |
37.5 | `color{blue}{sqrt(2 + sqrt( 2 - sqrt 3))/2 }` | `color{blue}{sqrt 6 + sqrt 3 - sqrt 2 - 2}` `color{blue}{= (sqrt 2 + 1)(sqrt 3 - sqrt 2)}` |
52.5 | 7 π 24 |
| π 4 |
45 | `color{blue}{sqrt 2/2}` | `color{blue}{1}` | 45 | π 4 |
|
cos(45°) = [ 0; 1, 2 ] cos2(45°) = [ 0; 2 ] | |||||
| 7 π 24 |
52.5 | `color{blue}{(sqrt(2 - sqrt( 2 - sqrt 3)))/2}` |
`color{blue}{sqrt 6 - sqrt 3 - sqrt 2 + 2}` `color{blue}{= (sqrt 2 - 1)(sqrt 3 + sqrt 2)}` |
37.5 | 5 π 24 |
| 3 π 10 |
54 | `color{blue}{(sqrt(10 - 2 sqrt 5))/4 = sqrt((5 - sqrt 5)/8)}` | `color{blue}{sqrt((5 + 2 sqrt 5)/5)}` | 36 | π 5 |
| cos2(54°) = [ 0; 2, 1, 8, 2 ] | tan2(54°) = [ 1; 1, 8, 2 ] | ||||
| π 3 |
60 | `color{blue}{1/2}` | `color{blue}{sqrt 3}` | 30 | π 6 |
|
cos(60°) = [0; 2] cos2(60°) = [0; 4] |
tan(60°) = [ 1; 1, 2 ] tan2(60°) = 3 | ||||
| 3 π 8 |
67.5 | `color{blue}{sqrt(2-sqrt 2)/2 = sqrt((4-sqrt 8)/8)}` | `color{blue}{1 + sqrt 2}` | 22.5 | π 8 |
| cos2(67.5°) = [ 0; 6, 1, 4 ] |
tan(67.5°) = [ 2; 2 ] tan2(67.5°) = [ 5; 1, 4 ] | ||||
| 2 π 5 |
72 | `color{blue}{(sqrt 5 - 1)/4 = sqrt((3-sqrt 5)/8)}` | `color{blue}{sqrt(5 + 2 sqrt 5)}` | 18 | π 10 |
|
cos(72°) = [ 0; 3, 4 ] cos2(72°) = [ 0; 10, 2, 8 ] | tan2(72°) = [ 9; 2, 8 ] | ||||
| 5 π 12 |
75 | `color{blue}{(sqrt 6 - sqrt 2)/4 = sqrt(1/2 - sqrt 3/4) = sqrt((4 - sqrt 12)/8)}` | `color{blue}{2+sqrt 3}` | 15 | π 12 |
| cos2(75°) = [ 0; 14, 1, 12 ] |
tan(75°) = [ 3; 1, 2 ] tan2(75°) = [ 13; 1, 12 ] | ||||
| 11 π 24 |
82.5 | `color{blue}{sqrt(2 - sqrt(2 + sqrt 3))/2}` | `color{blue}{sqrt 6 + sqrt 3 + sqrt 2 + 2}` `color{blue}{= (sqrt 2 + 1)(sqrt 3 + sqrt 2)}` |
7.5 | π 24 |
| π 2 |
90 | `color{blue}{0}` | `color{blue}{oo}` | 0 | 0 |
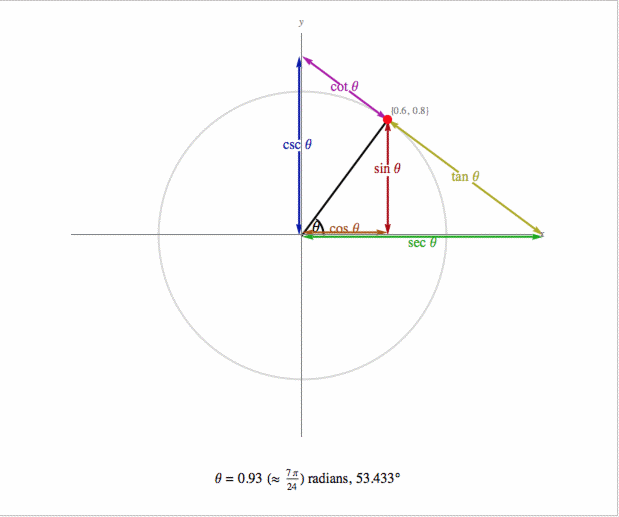
However, the diagram is useful for seeing what is measured by the six functions
but it does not give any indication of the signs of the values.
The signs are chosen to make the trig formula see below consistent for all angles. Also,
the next section shows their graphs and from the basic SINE graph, all the others follow.
The sine function
has many applications in mechanics (e.g. the motions of rotating objects),
electronics (e.g. alternating electric current and electromagnetic waves), ... .

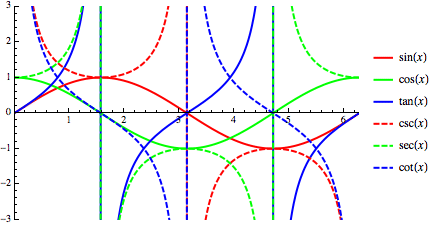
Sine |
All |
| Tangent |
Cosine |
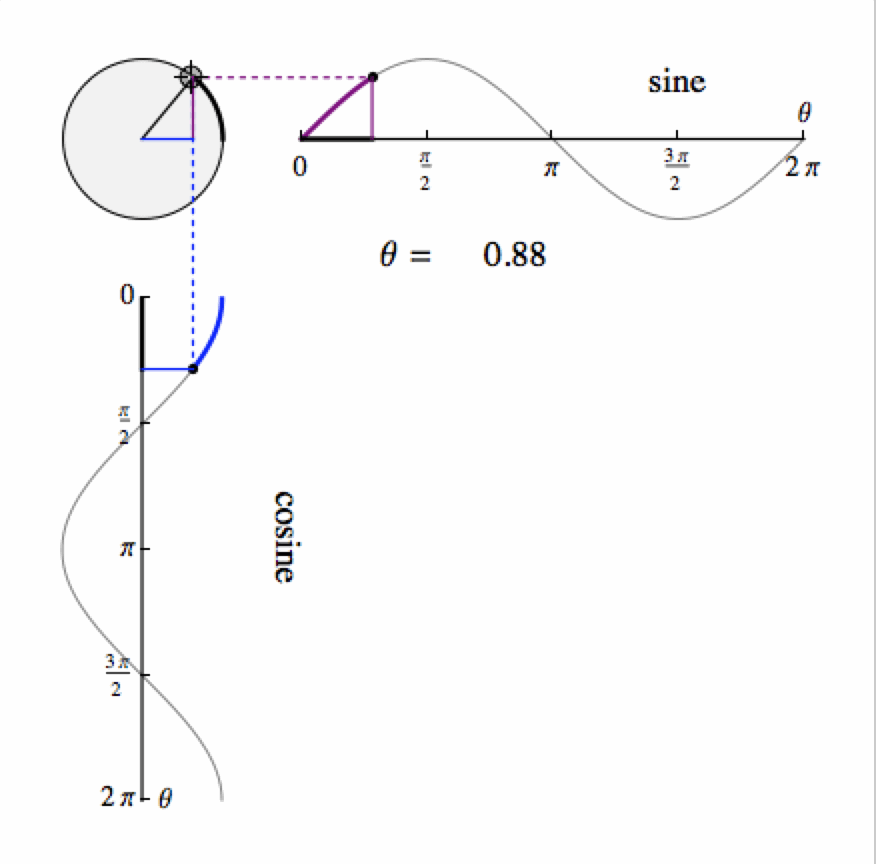 The basic formulae here all reply on the SINE graph as follows:
The basic formulae here all reply on the SINE graph as follows:
The angles can be measured by several types of unit.
| ° | rad | cosine | |||||||
|---|---|---|---|---|---|---|---|---|---|
| sine | ° | rad | |||||||
| 0 | 0 |
| 90 | π 2 | |||||
| 30 | π 6 |
| 60 | π 3 | |||||
| 45 | π 4 |
| 45 | π 4 | |||||
| 60 | π 3 |
| 30 | π 6 | |||||
| 90 | π 2 |
| 0 | 0 | |||||
|
|||||||||||||||||||||||||||||||||||||||||||
| cosine | |||
|---|---|---|---|
| sine | |||
| 2π 5 | 72° | `\color{blue}{frac{\sqrt{2 - \Phi}}{2}}` | 18° |
| 3π 10 | 54° | `\color{blue}{\frac{\sqrt{2 - \varphi}}{2}` | 36° |
| π 5 | 36° | `\color{blue}{\frac{\sqrt{2 + \varphi}}{2}}` | 54° |
| π 10 | 18° | `\color{blue}{\frac{\sqrt{2 + \Phi}}{2}` | 72° |
| cos(9°= π/20) = | `\color{blue}{ \frac{1}{2} \sqrt{2 + \sqrt{2 + \Phi}}` | = sin(81°) |
| cos(18°=π/10) = | `\color{blue}{\frac{1}{2} \sqrt{2 + \sqrt{2 + \varphi}} = \frac{1}{2}\sqrt{2 + \Phi}}` | = sin(72°) |
| cos(27°=3π/20) = | `\color{blue}{\frac{1}{2} \sqrt{2 + \sqrt{2 - \varphi}}}` | = sin(63°) |
| cos(36°=π/5) = | `\color{blue}{\frac{1}{2} \sqrt{2 + \sqrt{2 - \Phi}} = \frac{1}{2}\sqrt{2 + \varphi} = \frac{\Phi}{2}}` | = sin(54°) |
| cos(45°=π/4) = | `\color{blue}{\frac{1}{2} \sqrt{2 \pm \sqrt{2 - 2}} = \frac{\sqrt{2}}{2}}` | = sin(45°) |
| cos(54°=3π/10) = | `\color{blue}{\frac{1}{2} \sqrt{2 - \sqrt{2 - \Phi}} = \frac{1}{2}\sqrt{2 - \varphi}}` | = sin(36°) |
| cos(63°=7π/20) = | `\color{blue}{\frac{1}{2} \sqrt{2 - \sqrt{2 - \varphi}}}` | = sin(27°) |
| cos(72°=2π/5) = | `\color{blue}{\frac{1}{2} \sqrt{2 - \sqrt{2 + \varphi}} = \frac{1}{2}\sqrt{2 - \Phi} = \frac{\varphi}{2}}` | = sin(18°) |
| cos(81°=9π/20) = | `\color{blue}{ \frac{1}{2} \sqrt{2 - \sqrt{2 + \Phi}}}` | = sin(9°) |
| cos(0) | = | `\color{blue}{\frac{1}{2} \sqrt{2 + \sqrt{2 + 2}} = 1}` | sin(90°) |
| cos(7.5°=π/24) | = | `\color{blue}{\frac{1}{2} \sqrt{2 + \sqrt{2 + \sqrt{3}}}}` | sin(82.5°) |
| cos(37.5°=5π/24) | = | `\color{blue}{\frac{1}{2} \sqrt{2 + \sqrt{2 - \sqrt{3}}}}` | sin(52.5°) |
| cos(45°=π/4) | = | `\color{blue}{\frac{1}{2} \sqrt{2 \pm \sqrt{2 - 2}} = \frac{\sqrt{2}}{2}}` | sin(45°) |
| cos(52.5°=7π/24) | = | `\color{blue}{\frac{1}{2} \sqrt{2 - \sqrt{2 - \sqrt{3}}}}` | sin(37.5°) |
| cos(82.5°=11π/24) | = | `\color{blue}{\frac{1}{2} \sqrt{2 - \sqrt{2 + \sqrt{3}}}}` | sin(7.5°) |
| cos(90°=π/2) | = | `\color{blue}{\frac{1}{2} \sqrt{2 - \sqrt{2 + 2}} = 0}` | sin(0°) |
 |
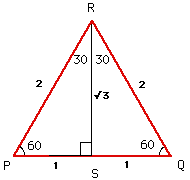 |
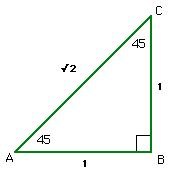
| This triangle is just a square cut along a diagonal. If the sides are of length 1, the diagonal is length √2. This gives the sin, cos and tan of 45°. | Here is an equilateral triangle where all sides and all angles are equal (to 60°). If the sides are of length 2, then when we cut it in half as shown, the two triangles have 60°, 30° and 90° angles with a side of length 1 and a hypotenuse of length 2. The other side is therefore of length √3. So we can read off the sin cos and tan of both 30° and 60°. |
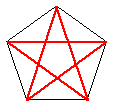 For 36° and 72° we need some further work based on the geometry of a regular pentagon
which has angles of 36° and 72°. If the sides of the pentagon are of length 1, the diagonals
are of the golden section number in length Phi where
For 36° and 72° we need some further work based on the geometry of a regular pentagon
which has angles of 36° and 72°. If the sides of the pentagon are of length 1, the diagonals
are of the golden section number in length Phi where
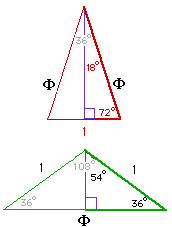 |
The upper triangle with angles 72°, 72° and 36° and sides of lengths 1, Phi and Phi
shows the trig values for 18° and 72°.
The lower triangle with angles of 36°, 36° and 108° and sides of lengths 1, 1 and Phi shows the trig values of 36° and 54°. | 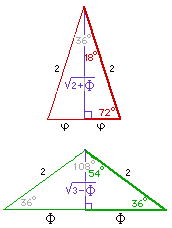 |
 |
 | ||
| a2 | = b2 + c2 – 2 b c cos(A) | ||
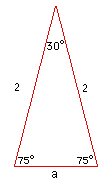
| For our triangle on the left, the known sides are b=2 and c=2 and the angle between them is A=30°. The length of the third side, the base a, is therefore: | |||
| a2 | = 22 + 22 – 2 x 2 x 2 x cos(30°) | ||
| = 8 – 4 √3 | |||
| = 2 (4 – 2 √3) | |||
| But (√3 – 1)2 = 3 + 1 – 2 √3 = 4 – 2 √3 and so | |||
| a2 | = 2 (√3 – 1)2 | ||
| Taking the square-root: | |||
| a | = √2 (√3 – 1) which we can also write as | ||
| = 2 (√3 – 1) / √2 | |||
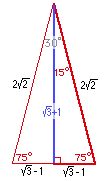
| Using this expressions for a, we can expand the triangle by a factor of √2, to get rid of the denominator. Finally, we put in a line from the top of the triangle to the centre of the base a to make two right-angled triangles. This will halve the side a and cut the triangle into two and gets rid of the factor 2 also. We then arrive at the triangle on the right which shows the sines and cosines of 75° and 15°: | |||
Here is another diagram with its lengths calculated easily. From it we can read that
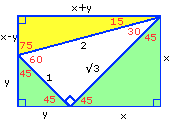
|
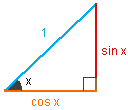
|
If we know the value of a trig function on two angles `a` and `b`, we can determine the trig function values of their sum and difference using the following identities:
|
`sin(a+b)=sin(a)cos(b)+cos(a)sin(b)` `cos(a+b)=cos(a)cos(b)-sin(a)sin(b)` |
`\color{blue}{tan(a+b)=(tan(a)+tan(b))/(1-tan(a)tan(b))}` | |
| `sin(a-b)=sin(a)cos(b)-cos(a)sin(b)` `cos(a-b)=cos(a)cos(b)+sin(a)sin(b)` | `\color{blue}{tan(a-b)=(tan(a)-tan(b))/(1+tan(a)tan(b))}` |
If the two angles are the same (i.e. `a=b`) we get the sines and cosines of double the angle. Rearranging those formulae gives the formula for the sin or cosine of half an angle:
| `\color{blue}{sin(2a)}` | `\color{blue}{=2sin(a)cos(a)}` | `\color{blue}{sin(a/2)=sqrt((1-cos(a))/2)}` | |
| `\color{blue}{cos(2a)` | `\color{blue}{=1-2sin^2(a)} ` | `\color{blue}{cos(a/2)=sqrt((1+cos(a))/2)}` | |
| `\color{blue}{ = cos^2(a)-sin^2(a)}` | |||
| `\color{blue}{=2 cos^2(a)-1}` | |||
| `\color{blue}{2 csc(2a) = tan(a) + cot(a)}` | `\color{blue}{tan(a/2) = (1-cos(a))/sin(a) = sin(a)/(1+cos(a))}` | ||
| `\color{blue}{sin(a) + sin(b) }` | `\color{blue}{= 2 cos((a-b)/2) sin((a+b)/2)}` | `cos(a) + cos(b) ` | `\color{blue}{= 2 cos((a-b)/2) cos((a+b)/2)}` | |
| `sin(a) - sin(b) ` | `\color{blue}{= 2 sin((a-b)/2) cos((a+b)/2)}` | `cos(b) - cos(a) ` | `\color{blue}{= 2 sin((a-b)/2) sin((a+b)/2)}` |
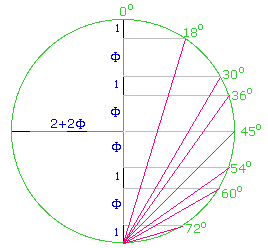 Robert Gray's page on Coordinates for many regular solids
has an amazing diagram at the bottom which relates Phi to the angles of 18°, 30°, 36°, 45°, 54°, 60° and 72° according to their
3D coordinates in the solids.
Robert Gray's page on Coordinates for many regular solids
has an amazing diagram at the bottom which relates Phi to the angles of 18°, 30°, 36°, 45°, 54°, 60° and 72° according to their
3D coordinates in the solids.
Each of those angles is measured from the top most point of the circle when a vertical line is turned through that angle.
Each line from the base point
meets the circle at a point whose a height is 1 (72°), 1+Phi (60°), 2+Phi (54°), 2+2 Phi (45°),
2+3 Phi (36°), 3+3 Phi (30°) or 3+4 Phi (18°).
Do look at his pages for more fascinating information on 120 3D solids, of which we will also explore the most symmetrical 5
on our next page.
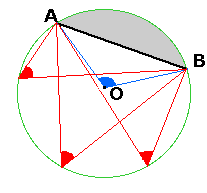
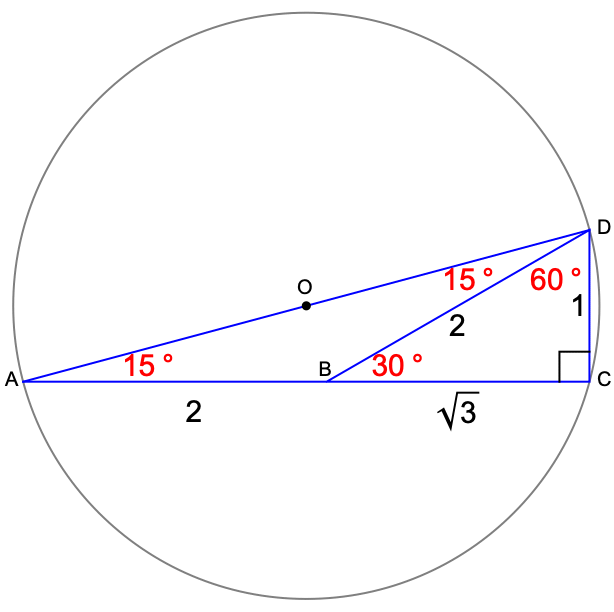
From any two points A and B on a circle, the angle AOB at the centre of a circle, O, is twice the angle at any point on the circumference in the same sector.
In the diagram,all the red angles at the circumference are equal;
the red angles
are half the blue angle AOB at the centre;
the red angles are to a point in the same sector of the circle as is the centre of the circle
so they cannot be in the grey sector.
Carl Friedrich GAUSS (177 - 1855) looked at a similar problem which answers this question.
He investigated if there
was a method of constructing a regular polygon of n sides using only a pair of compasses
(to draw circles) and a straight-edge
(a ruler with no markings). We know we can construct a regular polygon for all of the
values of n=3, 4, 5, 6, 8 and 10.
The Trig Formula section above contains a formula for the cosine of half an angle in terms of the cosine of the (whole) angle:
`\color{blue}{cos(pi/4)}` = `\color{blue}{(sqrt 2)/2}`However, this page is about sines and cosines which have simpler expressions, so we will not expand on this except to say that it shows how we can always find an exact expression for the sine (or cosine) of `1/2, 1/4, 1/8, ... ,1/2^n` of any angle for which we have an exact sine (or cosine) expression.
`\color{blue}{cos(pi/8)}` = `\color{blue}{(sqrt (2+sqrt 2))/2}`
`\color{blue}{cos(pi/16)}` = `\color{blue}{(sqrt(2+sqrt (2+sqrt 2)))/2}`
`\color{blue}{cos(pi/32)}` = `\color{blue}{(sqrt(2+sqrt(2+sqrt (2+sqrt 2))))/2}`
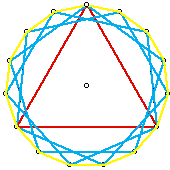 If we construct a regular triangle (3 sides) and with the same circle centre, construct
three regular pentagons (5 sides) with each having one vertex in common with the triangle,
we will have the 15 vertices of a regular 15-gon.
If we construct a regular triangle (3 sides) and with the same circle centre, construct
three regular pentagons (5 sides) with each having one vertex in common with the triangle,
we will have the 15 vertices of a regular 15-gon. In the next 2000 years no one found an exact geometric method for 7-gons or 9-gons but also no one had proved it was impossible to construct such regular polygons.
Then C F Gauss completely solved the problem while he was a student at Göttingen between 1795 and 1798. Gauss found the conditions on n and its prime factors to solve two equivalent problems:
Prime numbers of the form 22k+1 are called Fermat primes. The series of numbers of the form 22k+1 begins
Such numbers, n, of the form Gauss describes are as follows, one per row, each a product of some of the Fermat primes (but each prime at most once) followed by its multiples of two. For any number in the table, its double is also in the table:
| 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | ... | |
| 3 | 6 | 12 | 24 | 48 | 96 | 192 | ... | ||
| 5 | 10 | 20 | 40 | 80 | 160 | ... | |||
| 3×5= | 15 | 30 | 60 | 120 | 240 | ... | |||
| 17 | 34 | 68 | 136 | 272 | ... | ||||
| 3×17= | 51 | 102 | 204 | 408 | ... | ||||
| 5×17= | 85 | 170 | 340 | 680 | ... | ||||
| 3×5×17= | 255 | 510 | 1020 | 2040 | ... | ||||
| 257 | 514 | 1028 | 2056 | ... |
The odd terms (the left hand column apart from 2) is the series
Some interesting facts about these odd numbers (we include 1 here too) are:
|
|
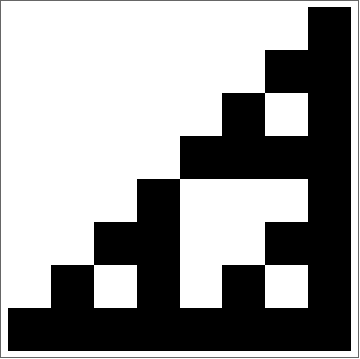
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| the odd numbers |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
every element is generated by
adding together the two elements on the row above: the one directly above and the one to the right. |
|
|
if both the elements on the row above are the same colour: both black (odd) or both white (even) the element will be white (even) |
if the two elements on the row above are different one odd, one even the element is black (odd) | ||||||||||||||||||
|
|
| `\color{blue}{cos(pi/17)} ` | `\color{blue}{= sqrt(15+sqrt 17 + sqrt(34 - 2 sqrt 17) + sqrt(68+12 sqrt 17 - 4 sqrt(170 + 38 sqrt 17)))/(4 sqrt(2))}` |
| `\color{blue}{= 0.98297309968390177828194884485...}` |
| `\color{blue}{A_(+) = 15 + sqrt(17)}` | `\color{blue}{A_(-) = 15 - sqrt(17)}` | |
| `\color{blue}{B_(+) = sqrt(2) sqrt(17+sqrt(17))}` | `\color{blue}{B_(-) = sqrt(2) sqrt(17 - sqrt(17))}` | |
| `\color{blue}{C_(+) = 17 + 3 sqrt(17)}` | `\color{blue}{C_(-) = 17 - 3 sqrt(17)}` | |
| `\color{blue}{D_(+) = sqrt(2) sqrt(85+19 sqrt(17))}` | `\color{blue}{D_(-) = sqrt(2)sqrt(85 - 19 sqrt(17))}` |
| a | √32 cos2(a) |
|---|---|
| `color{blue}{pi/17}` | `color{blue}{A_(+)+B_(+)+2 sqrt(C_(+)-D_(+))}` |
| `color{blue}{{2 pi}/17}` | `color{blue}{A_(+)-B_(-)+2 sqrt(C_(+)+D_(+))}` |
| `color{blue}{{3 pi}/17}` | `color{blue}{A_(-)+B_(+)+2 sqrt(C_(-)+D_(-))}` |
| `color{blue}{{4 pi}/{17}}` | `color{blue}{A_(+)+B_(-)-2 sqrt(C_(+)-D_(+))}` |
| `color{blue}{{5 pi}/{17} }` | `color{blue}{A_(-)+B_(+)-2 sqrt(C_(-)+D_(-))}` |
| `color{blue}{{6\pi}/{17} }` | `color{blue}{A_(-)-B_(+)+2 sqrt(C_(-)-D_(-))}` |
| `color{blue}{{7\pi}/{17} }` | `color{blue}{A_(-)-B_(+)-2 sqrt(C_(-)-D_(-))}` |
| `color{blue}{{8\pi}/{17}}` | `\color{blue}{A_(+)-B_(-)-2 sqrt(C_(+)+D_(+))}` |
The next value with an odd denominator is π/257 and the exact expression for cos(π/257) using square-roots only will be even more complicated!
Tom Ace pointed out that there is more about this in chapter 15 of Oystein Ore's Number Theory and Its History from 1948 and now available as a Dover book (1988).
| `color{blue}{A_(+)=9+sqrt 5}` | `color{blue}{A_(-)=9 - sqrt 5}` | |
| `color{blue}{B_(+)=sqrt(6(5+sqrt 5))}` | `color{blue}{B_(-)=sqrt(6(5-sqrt 5))}` |
| a | 4cos2(a) |
|---|---|
| π 15 |
`color{blue}{A_(+)+B_(-)}` |
| 2π 15 |
`color{blue}{A_(-)+B_(+)}` |
| 4π 15 |
`color{blue}{A_(+)-B_(-)}` |
| 7π 15 |
`color{blue}{A_(-)-B_(+)}` |
For other values, such as `\color{blue}{cos(pi/8)}`, type in and evaluate it first as a decimal
and then as a continued fraction showing that the CF is
[0; 1, 12, 7, 3, 2, 1, 1, 1, 1, 20, 5, 3, 11, 1, 7, 7, 3,...]. Even looking ahead for many more terms
there is no pattern here.
However, if we change the Expression to Evaluate to
the CF this time is
[0; 1, 5, 1, 4, 1, 4, 1, 4, 1, 4, 1, 4,...].
There is a clear pattern here that goes on for many terms. If we delete the 1,4,1,4,... part and put it into the recurring part
input for the CF
so that you have the CF [0; 1, 5, ] and then pressing the convert-to-fraction-form button
() will show `\color{blue}{(2+sqrt(2))/4}` as the value of `cos(pi/8)^2` and so we deduce that (computationally)
`\color{blue}{cos(pi/8)=sqrt(2+sqrt(2))/2}`.
In this way we can experimentally discover many such expressions for trig forms
using the ability of this Calculator to quickly evaluate
to many decimal places and to (accurately and exactly) convert continued fractions to the form
`(a\pm sqrt(b))/c`.
Then we can look for a mathematical proof
that our results are indeed true.
Change the Working Precision to 50, 100, or even 200 dps to see if patterns persist with more computational accuracy.