1·61803 39887 49894 84820 45868 34365 63811 77203 09179 80576 ..More.. ![]()
[There are other shapes that make fair
dice if we relax these conditions a little. Can you guess what they are?
See the footnote for the answers.]
There are only FIVE fair-dice-shapes altogether
if we strictly insist on the following conditions:
Their names come from the number of faces (hedron=face in Greek and its plural is hedra). tetra=4, hexa=6, octa=8, dodeca=12 and icosa=20.
Remember that in these pages Phi is 1·61803.. and phi is 1/Phi = Phi-1 = 0·61803... .
The Solid images can be rotated ( press the button) as can the Stereo views.
For the auto-stereographic views, either cross your eyes or keep your eyes focussed in the distance until the
two images fuse into one and you see the shape in depth. If you
place your mouse on the "rotate" button before
you do this then a quick click will make it appear to rotate in 3-dimensions.
You may notice a pause when first seeing a rotating diagram while it is being
downloaded.
The "wire-frame" views are symmetrical plan views of the frame of the object with wire edges and the faces missing, dotted lines being edges that would be hidden by solid faces.
| Solid View |
Stereo View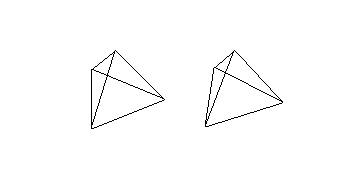 |
Wireframe Views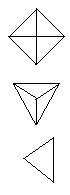 |
|
4 vertices with coordinates: (1, 1, 1), (1, -1, -1), (-1, 1, -1), (-1, -1, 1) 6 edges of length 2 4 triangular faces, Surface area = 8 √3, volume = 8/3, | ||
| Solid View |
Stereo View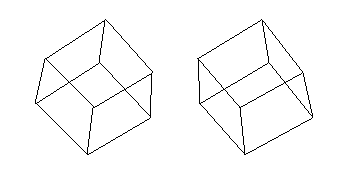 |
Wireframe Views |
|
8 vertices with coordinates (±1, ±1, ±1), i.e.:
(1, 1, 1), (1, 1, -1), (1, -1, 1), (1, -1, -1), (-1, 1, 1), (-1, 1, -1), (-1, -1, 1), (-1, -1, -1) 12 sides of length 2, mid point of edge to centre of solid = √2 6 square faces each of area 4, surface area = 24, volume 8 | ||
| Solid View |
Stereo View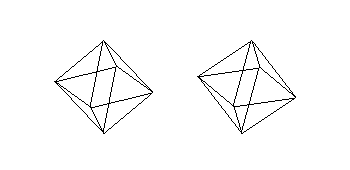 |
Wireframe Views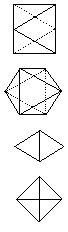 |
|
6 vertices with coordinates (±1, 0 0), (0, ±1, 0), (0, 0, ±1) i.e.:
(1, 0, 0), (-1, 0, 0), (0, 1, 0), (0, -1, 0), (0, 0, 1), (0, 0, -1) 12 sides of length 8 triangular faces, surface area = 4√3, volume 4/3 | ||
| Solid View |
Stereo View |
Wireframe Views |
|
20 vertices with coordinates (0, ±phi, ±Phi),(±Phi, 0, ±phi),(±phi, ±Phi, 0),
(±1, ±1, ±1), i.e.: (0, phi, Phi), (0, phi, -Phi), (0, -phi, Phi), (0, -phi, -Phi), (Phi, 0, phi), (Phi, 0, -phi), (-Phi, 0, phi), (-Phi, 0, -phi), (phi, Phi, 0), (phi, -Phi, 0), (-phi, Phi, 0), (-phi, -Phi, 0), (1, 1, 1), (1, 1, -1), (1, -1, 1), (1, -1, -1), (-1, 1, 1), (-1, 1, -1), (-1, -1, 1), (-1, -1, -1) 30 sides of length 2 phi, mid point of edge to centre of solid = Phi, vertex to centre = 12 pentagonal faces, surface area = 12 √5 phi = √360(5 − √5) = 15 √5 Phi + 10 , volume = 8 + 4 Phi = 10 + 2 | ||
Solid View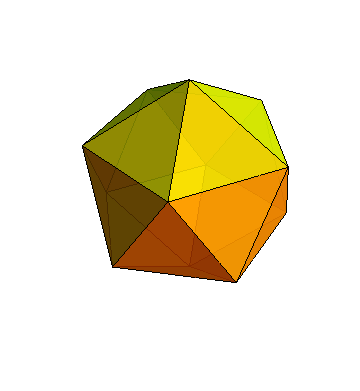 |
Stereo View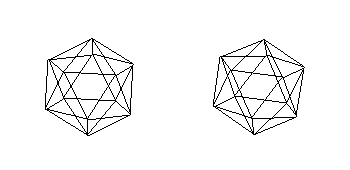 |
Wireframe Views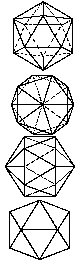 |
|
12 vertices with coordinates (0, ±Phi, ±1), (±1, 0, ±1Phi),
(±Phi, ±1, 0) i.e.: (0, Phi, 1), (0, Phi, -1), (0, -Phi, 1), (0, -Phi, -1), (1, 0, Phi), (1, 0, -Phi), (-1, 0, Phi), (-1, 0, -Phi), (Phi, 1, 0), (Phi, -1, 0), (-Phi, 1, 0), (-Phi, -1, 0) 30 sides of length 2, mid point of edge to centre of solid = (1+Phi)/ 20 triangular faces, Surface area = 20 | ||
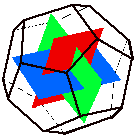
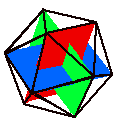 If we join mid-points of the dodecahedron's faces,
we can get three rectangles all at right angles to each other. What's more, they are
Golden Rectangles since their edges are in the ratio 1 to Phi.
If we join mid-points of the dodecahedron's faces,
we can get three rectangles all at right angles to each other. What's more, they are
Golden Rectangles since their edges are in the ratio 1 to Phi. 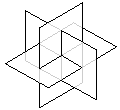 Using these golden rectangles it is easy to see that
the coordinates of the icosahedron are as given above since they are:
Using these golden rectangles it is easy to see that
the coordinates of the icosahedron are as given above since they are:
+--------------+ Make and one +-------------+
! ! two of ! !
! ====== ! of these ! ===========
! ! these ! !
+--------------+ +-------------+
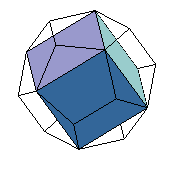 We can see a cube in a dodecahedron if we use one diagonal on each face. Since
the diagonals of a dodecahedron are Phi times as long as the sides (see
Pentagons and Pentagrams on the Phi and 2D Geometry
page at this site), then cube's
sides and the dodecahedron's sides are in the golden ratio.
We can see a cube in a dodecahedron if we use one diagonal on each face. Since
the diagonals of a dodecahedron are Phi times as long as the sides (see
Pentagons and Pentagrams on the Phi and 2D Geometry
page at this site), then cube's
sides and the dodecahedron's sides are in the golden ratio.
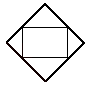
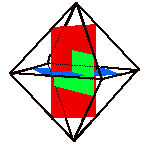 Using the same three golden rectangles at right-angles to each other, we can also make
an octahedron.
Using the same three golden rectangles at right-angles to each other, we can also make
an octahedron. 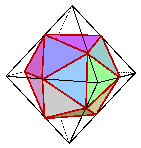 Now if we join the "golden-section points" forming the corners of
our three rectangles (and now on both the edges of an octahedron
and also forming the vertices of an icosahedron as we saw above), we can
see how to fit an icosahedron into an octahedron - and the process involves
golden sections!
Now if we join the "golden-section points" forming the corners of
our three rectangles (and now on both the edges of an octahedron
and also forming the vertices of an icosahedron as we saw above), we can
see how to fit an icosahedron into an octahedron - and the process involves
golden sections!
Here are some more Platonic-solids-within-Platonic-solids:
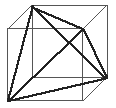
A Tetrahedron in a Cube
Select one corner of a cube and join it
to the opposite corner on each face.
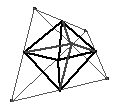
An Octahedron in a Tetrahedron
Join the mid-point of each edge to any other
edge mid-point where the connecting line lies on one face of the tetrahedron.
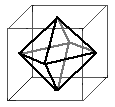
An Octahedron in a Cube
Join the mid-points of faces: if two faces are
next to each other at a corner, then their mid-points can be joined.
 The Greeks saw great significance in the existence of just 5 Platonic solids and they
related them to the 4 ELEMENTS (fire, earth, air and water) that they thought
everything was made from. Together with the UNIVERSE, they associated each with a particular solid.
The Greeks saw great significance in the existence of just 5 Platonic solids and they
related them to the 4 ELEMENTS (fire, earth, air and water) that they thought
everything was made from. Together with the UNIVERSE, they associated each with a particular solid.
Of the 5 solids, the tetrahedron has the smallest volume for its surface area and the icosahedron the largest; they therefore show the properties of dryness and wetness respectively and so correspond to FIRE and WATER.Kepler called the golden section "the division of a line into extreme and mean ratio", as did the Greeks. He wrote the following about it:
The cube, standing firmly on its base, corresponds to the stable EARTH but the octahedron which rotates freely when held by two opposite vertices, corresponds to the mobile AIR.
The dodecahedron corresponds to the UNIVERSE because the zodiac has 12 signs (the constellations of stars that the sun passes through in the course of one year) corresponding to the 12 faces of the dodecahedron.
"Geometry has two great treasures: one is the Theorem of Pythagoras; the other, the division of a line into extreme and mean ratio. The first we may compare to a measure of gold; the second we may name a precious jewel."
Johannes Kepler, (1571-1630)
1·61803 39887 49894 84820 45868 34365 63811 77203 09179 80576 ..More.. ![]()
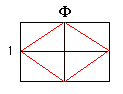 The surprising relationship
that holds for these new rhombuses is that
The surprising relationship
that holds for these new rhombuses is that
The two solids are similar to a cube but the faces are golden rhombs.
The first shape is made by attaching three golden rhombs at their shorter
angles in the same way as three squares meet at
a corner of a cube. A duplicate is made and the two fit
together to make a six-sided shape like a slanted cube.
This is called a prolate rhombohedron.
The other shape is made by joining three golden rhombs together in the same way but
at the larger angles this time. A duplicate of this is again fitted to make a different
six-sided cube-like shape. This is called an oblate rhombohedron.
The two shapes look like cubes leaning over to one side.
Take a large number of one of these shapes and you can indeed fill as large a
space as you like with them.
When stacking cubes or octahedra, all the shapes are aligned
identically (look identical, with the same orientation).
When we use a rhombohedron, some must be turned round to fit in with others.
These also occur in nature, although only discovered since the 1950's
and, because they are not quite as symmetrical as crystals, as called
quasi-crystals.
Crystals, the most symmetrical structures (with identical orientation for all the building
blocks) are seen in sugar and salt as well as diamonds and quartz.
Quasicrystals are an unsuspected new state of matter, sharing some of the properties
of crystals and also on non-crystalline matter (such as glass). In 1984 the "impossible"
five-fold symmetry was observed in an aluminium-manganese alloy (Al6Mn)
and the term
quasicrystal was invented for it in:
![]() D Shechtman, I Blech, D Gratias, J W Cahn Metallic
phase with long-range orientational order and no translational
symmetry Physics Review Letters 1984, Vol 53, pages 1951-1953.
D Shechtman, I Blech, D Gratias, J W Cahn Metallic
phase with long-range orientational order and no translational
symmetry Physics Review Letters 1984, Vol 53, pages 1951-1953.
 |
 |
||
| Domino | 2 Triominoes | 5 Tetrominoes | 12 Pentominoes |
Let no one ignorant of geometry enter hereAs a philosopher, he held the view that mathematical objects "really" existed so that they are discovered by mathematicians (in the same way that new continents are discovered by explorers) rather than invented in the way that the TV or computer were invented. Plato believed that mathematics provided the best training for thinking about science and philosophy. The five regular solids are named "Platonic Solids" today after Plato.
Things that are equal to the same thing are equal to each other.From these, Euclid proved theorems such as
The whole is greater than the part.
It is possible to draw a circle with any point as centre and with any radius.
It is possible to draw a straight line between any two points.
The angles in a triangle add up to two right angles.One of Euclid's aims in his Elements seems to be to prove that there were only 5 solid (i.e. 3-dimensional) objects with all sides equal and all angles equal, and this occupies the final (13th) book of the Elements.
The 13 books - now available in English in a 3-volume set -
are classics is every sense!
 We saw above that the Greeks knew of the 5 shapes that make fair dice.
The Romans used a cubic dice and this is the one we most often use today.
We saw above that the Greeks knew of the 5 shapes that make fair dice.
The Romans used a cubic dice and this is the one we most often use today.
Should we say one die or one dice?
The dictionary says that die is singular and dice is its plural form, so we ought to speak of throwing a die or two dice.
These days the plural word dice is often used for one die and the dictionary recognises this also.
A popular gambling game from at least Roman times involved throwing dice and is also called casting the dice. Some of the Roman soldiers "cast lots" for the clothes of Jesus at his crucifiction. Today we still use the phrase the die is cast. I used to think this phrase meant that a mould (US spelling=mold) had been made since we also read of someone being cast in the heroic mould as if they had been molten metal poured into a mould from which they solidify into a heroic shape. However I was wrong and it is just another use of the word die.
The real meaning of the phrase the die is cast is that a dice (one!) has been thrown (cast) meaning that, as in a game of chance, "the outcome is now fixed, the decision is made".
In these pages, I shall stick to the popular and common use, and make dice refer to the singular as well as the plural.
From the Platonic solids that we saw above, we have dice of
4 sides : the tetrahedronThere are other shapes if we don't insist that all the sides are the same length OR we allow 2-D shapes, but which still are fair dice - i.e. each number on a face is as likely as any other number to turn up.
6 sides: the cube (or hexahedron)
8 sides: the octahedron
12 sides: the dodecahedron
20 sides: the icosahedron
If we let sides be different lengths, we can have a prism which is like a
new (unsharpened) pencil with flat sides.
 Often pencils have just 6 flat sides, and we roll the pencil so that any side
is likely to be face up. We can imagine a pencil with 8 sides, or 7 or even 27.
If we have an odd number of sides, no one face is "up" (consider a triangular cross-sectioned
pencil for instance, with just 3 choices of side). Here we may agree to use the side that
the pencil lands on.
Often pencils have just 6 flat sides, and we roll the pencil so that any side
is likely to be face up. We can imagine a pencil with 8 sides, or 7 or even 27.
If we have an odd number of sides, no one face is "up" (consider a triangular cross-sectioned
pencil for instance, with just 3 choices of side). Here we may agree to use the side that
the pencil lands on.
The other range of shapes is the spinner that comes with some boxed games.
 Here we have a flat polygon with all sides of the same length (to make it fair). This was
not in our list of Platonic solids because it is not a solid - it is just a flat 2-dimensional
shape.
However, we can have any number of sides and each is equally likely to be
the side the spinner lands on, so it is fair.
Here we have a flat polygon with all sides of the same length (to make it fair). This was
not in our list of Platonic solids because it is not a solid - it is just a flat 2-dimensional
shape.
However, we can have any number of sides and each is equally likely to be
the side the spinner lands on, so it is fair.
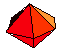 Putting both of the above shapes together, we get a dice which is two n-gon-al
pyramids, joined at their bases (the n-gons) to form a double pyramid or
bi-pyramid.
The picture shows a 12-sided dice formed
from two 6-sided pyramids joined at their hexagonal bases.
Perhaps we should call it a bi-hexahedral dice.
Putting both of the above shapes together, we get a dice which is two n-gon-al
pyramids, joined at their bases (the n-gons) to form a double pyramid or
bi-pyramid.
The picture shows a 12-sided dice formed
from two 6-sided pyramids joined at their hexagonal bases.
Perhaps we should call it a bi-hexahedral dice.
If we used pentagons then the bi-pyramidal dice would be 10-sided.
It would be useful for generating random numbers up to 10.
By using two of them,
say a red one for tens digits and a
green one for units digits,
we can roll random numbers from the hundred values between
00 and
99.
If we added a blue one also,
then we can get up to
999, and so on.
The advantage of the bi-pyramidal dice is that there is always a side on top no matter how the dice lands.
With thanks to Robert Popa for recommending the following:
More isohedral (i.e same-faced) dice
where the edge lengths are not equal but the faces are all identical.
You can purchase some of these non-standard dice at Game shops or online, for example at
Crystal Caste .
 The Mathematical Magic of the Fibonacci Numbers
The Mathematical Magic of the Fibonacci Numbers
|
WHERE TO NOW??? |
The next topic is... |