Phi's Fascinating Figures
On this page we meet some more marvellous maths about the number Phi itself, its
multiples and powers.
The calculators on this page require JavaScript.
If JavaScript is enabled then this panel will disappear in a few seconds.
If you have switched JavaScript off (if it is disabled) then please go to the
Preferences for this browser and enable it if you want to use the
calculators, then Reload this page.
Contents of this page
The

icon means there is a
You do the maths... section of questions to start your own investigations.
The

calculator icon
indicates that there is a live interactive calculator in that section.
1·61803 39887 49894 84820 45868 34365 63811 77203 09179 80576 ..More.. 
Powers of Phi
We return to the definition of Phi, as the positive valued solution to
P(P-1)=1
P here is either of 2 values, Phi and 1-Phi.
So P has the property that P2=P+1.
Let's look at Phi2 first.
Phi squared
We can read the equation above as
to find P2, just add 1 to P.
You do the maths...

- Use your calculator to evaluate Phi=(1+
 5)/2.
If you have a Memory on your calculator, store this value in it.
5)/2.
If you have a Memory on your calculator, store this value in it.
- Square it and check that it is just Phi+1 (i.e. subtract one and compare with the
Memory value).
- Use your calculator to evaluate the other value (1-Phi) or (1-Memory) =
(1-
 5)/2
5)/2
- Again square the value just found and check that it is just the same as
adding 1 to the value you squared.
Now let's look at Phi3.
Phi cubed
Is there another way to calculate Phi3 apart from just Phi x Phi x Phi?
Yes - let's see how to compute it in two more ways.
We use the basic P(P-1)=1 formula or, in another form,
P2=P+1.
P3 is just P.P2
= P(P+1) by our "basic formula", which expands to
P2+P
...now that's interesting!...
1 + P = P2 AND
P + P2 = P3
...hmmm! Is there anything in this do you think?
Question: How could this be generalized?
We'll use this result in the next sub-section about a Phi-bonacci Brick...
but, for now, let's get back to the original equation...
and P2 + P = (P+1) + P after using the "basic formula" again
and this is just 2P + 1. So
Phi3 = 1 + 2 Phi
Notice that this needs just one multiplication rather than two if
we evaluated Phi x Phi x Phi. That's the first quick way.
The second answer was spotted by Scott Beach but it is also
in the table at the foot of this page:
since Phi=(√5+1)/2 then 2Phi is √5+1
and 1+ 2 Phi = &radic 5 + 2:
Phi3 = 2 + √5
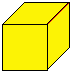
Interesting Facts about a Phi-bonacci Brick
[This variation was suggested by Hud Nordin of Sunnyvale, California.]
 If we have a brick with sides of lengths 1, Phi=1·61803...
and phi=1/Phi=0·61803... then:-
If we have a brick with sides of lengths 1, Phi=1·61803...
and phi=1/Phi=0·61803... then:-
- the longest side is the sum of the other two lengths
since 1 + phi = Phi
- the largest face (area C=1 x Phi) is the sum of the other
two face's areas (area A =1 x phi and area B=phi x Phi) since
Area A + Area B
= 1 x phi + phi x Phi
= phi + 1
= Phi
= Area C
The next three interesting facts and figures on the Phibonacci brick
were first pointed out by
Donald Seitz in The Mathematics Teacher, 1986, pages 340-341 in an article
entitled A Geometric Figure Relating the Golden Ratio to Pi.
- What is the surface area S of the brick?
Above we saw that
the sum of the 2 smaller face's areas equals the largest face's area,
and that this is Phi.
Since there are 2 faces with smallest area, 2 of middle-sized area
(which total 2 times the largest face area, that is 2 Phi) and we also have
two other faces of the largest area (Phi) , then:
The surface area of the brick is 4 Phi
- How long is the diagonal across the brick?
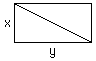 Another surprise awaits us when we calculate the length of the diagonal
across the brick.
Another surprise awaits us when we calculate the length of the diagonal
across the brick.
The formula is a 3-dimensional analogue of Pythagoras Theorem.
For a rectangle of sides x and y, its diagonal is
 (x2 + y2).
(x2 + y2).
For a 3-D brick with sides x,y and z, its diagonal has length
 (x2 + y2 + z2).
(x2 + y2 + z2).
So how long is the diagonal of our Phi-bonacci brick? Since its sides (x,y and z)
are 1, Phi and phi, the length of its diagonal is:
 (12 + Phi2 +
phi2).
I'll leave you to check the algebra but the surprisingly simple answer is
(12 + Phi2 +
phi2).
I'll leave you to check the algebra but the surprisingly simple answer is
The diagonal of the brick has length 2
- A relationship between Phi and Pi
 Even more surprising is that the brick shows a simple relationship between Pi
and Phi, using the values for the diagonal D that we have just found
and the surface area S.
Even more surprising is that the brick shows a simple relationship between Pi
and Phi, using the values for the diagonal D that we have just found
and the surface area S.
If we imagine the brick tightly packed into a sphere, the centre of the
sphere will be half way along diagonal D.
So the radius of the sphere will be 1 and
its surface area will be 4 Pi.
We showed above that the surface area of the brick, S, is 4 Phi.
Putting these two together we have:
The ratio of the surface areas of
the Phibonacci brick and
its surrounding sphere
is Phi : Pi
You do the maths...

- Suppose we have a brick with sides a, b and c. Suppose also that the sum of
the smaller sides equals the longest side (i.e. that a+b=c). Also suppose we have the
"Area sum property" too, that the smaller two areas add up to the larger, or that
ab + ac = bc. The questions here show that the only way to
have BOTH properties is when a and b as well as b and c are in the golden ratio (Phi):-
Show that, if we let k stand for a/b then we must also have k = b/c .
- Show that k must also satisfy k2 = 1 + k
- ... and hence show that k must be Phi.
- Golden Triangles, Rectangles and Cuboids by M Bicknell and V E Hoggatt Jr in
Fibonacci Quarterly vol 7 (1969), pages 73-91
is a very readable account of some generalizations of these results.
The Golden rectangle and powers of phi
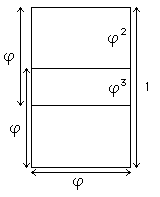 On a golden rectangle with sides of length phi and 1,
dividing at the golden ratio point gives two overlapping
squares whose sides are phi.
On a golden rectangle with sides of length phi and 1,
dividing at the golden ratio point gives two overlapping
squares whose sides are phi.
The gap between a square and the longer side has
length 1-phi which is also phi2.
So the phi by phi squares are themselves divided at their own
golden section ratios by the side of the other overlapping square.
The size of the overlap is phi-phi2 which is just
phi3 (because the equation 1-phi=phi2
can be multiplied by phi to give the relation phi-phi2
= phi3).
As an exercise, how would you easily construct a line of
length phi4 = phi2-phi3 on the diagram?
Higher powers of phi
Here is another geometrical illustration of phi2, phi3 and
phi4:
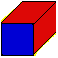
 If we take a square with sides of length 1 and divide two sides at the
golden section point, we form two new squares (yellow and blue)
and two (red) rectangles.
Notice that the diagonal is also
divided at its golden section point too.
If we take a square with sides of length 1 and divide two sides at the
golden section point, we form two new squares (yellow and blue)
and two (red) rectangles.
Notice that the diagonal is also
divided at its golden section point too.
The large yellow square has sides of length phi, so its area is
phi2.
The sides of a red rectangle are of length phi
and 1-phi=phi2 so each has an area
of phi3!
The small blue square has sides of length 1-phi=phi2
so its area is phi4!!
So, the squares plus the rectangles area must add up to 1, the area of the
big square and we have yellow + 2 blue + red = 1:
1 = phi2 + 2 phi3 + phi4
You do the maths...

- Evaluate Phi and raise it to the power 4 (hint: square it twice) on your calculator.
Save this value in a memory (or write it down).
- Compare the value you have just found with (3 Phi+2).
- What is Phi5 in the form
a Phi + b (ie find the integers a
and b) ?
- Write Phi6 in the same form.
- Can you spot a general pattern for Phin?
Hint: spot the well-known series for the values of a and b
in the successive powers of Phi?
-
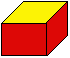
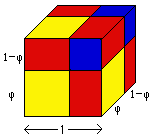 Here is a cube with sides divided at the golden section points to
split it into eight pieces.
The eight pieces are of 4 different shapes:
There are 8 blocks in the cube: how many of each shape are there?
Here is a cube with sides divided at the golden section points to
split it into eight pieces.
The eight pieces are of 4 different shapes:
There are 8 blocks in the cube: how many of each shape are there?
What is the volume of each?
( Each volume will be a power of phi!)
If the total volume is 1 (since the original cube has sides of length 1),
what relationship does this suggest between your multiples of powers of phi
and 1?
-
Expand (1+phi)3. Since 1+phi=phi-1 your answer will
also equal (phi-1)3=phi-3.
How is this answer related to the relationship you found in the last question?
A relation on Powers of Phi
There's an even more intriguing relationship between the powers of Phi than the
one you discovered for yourself in the last section. Here's how you can find it:
You do the maths...

- What do you notice about the difference between
Phi3 and Phi2?
- and how does Phi4-Phi3
compare with another power of Phi?
- Can you guess what we must add to Phi4
to get Phi5.
- What is the general pattern:
Phin = Phin-1 + ?
- Can you justify this using your answer to the last section?
that is, using your pattern for
Phin = a Phi + b
1·61803 39887 49894 84820 45868 34365 63811 77203 09179 80576 ..More.. 
Multiples of Phi
We've just seen that we can use multiples of Phi to calculate its powers easily
and you might think that there's not much else we can discover about multiples of Phi.
Here we show another relationship and also explain how the
Rabbits family Tree diagram was made,
originally seen in the Fibonacci and Nature.
It's all to do with the multiples of Phi, or,
rather, the fractional parts of the multiples.
You do the maths...

- On a piece of paper, draw a line 10cm long near the top, or use graph paper.
This is going to be used to
plot the fractional parts of the multiples of Phi=1·618.. so it
will represent values from 0 to 1 (0·5 being at 5cm, 1 at 10cm etc).
- Draw the first point at the fractional part of Phi itself=0.618, ie
at 6·18 cm along the line. Mark it 1, since we used 1 times Phi.
- Draw another line underneath the first. On it put a point for the fractional
part of 2Phi=3.236 ie at 2·36cm. Mark the point as 2.
- Draw another line underneath the last. On it put a point for the fractional
part of 3Phi=4.854, ie at 8·54cm. Mark it as 3.
- Draw a new line and this time mark TWO points labelled 4 and
5,
so that this line will have the next
2 multiples of Phi: 4Phi and 5Phi.
- The next line will have the next THREE multiples of Phi:
6Phi, 7Phi and 8Phi.
- The next line will have the next FIVE multiples of Phi.
- The next line will have the next EIGHT multiples of Phi.
- ..you can guess the next one!
- When you're tired of drawing lines and plotting points,
add some thick vertical lines down from each point.
- Where each vertical line begins, draw a thick horizontal line
to the nearest vertical line.
We can interpret the thick lines of the Rabbit Family Tree as follows:
- The 10 cm lines across the page each represent one new generation of rabbits,
or each new month in Fibonacci's original problem.
- Each thick vertical line represents one of our rabbit pairs and..
- .. each pair is "born" when it appears for the first time as a branch from an
thick vertical line that started higher up the page (its "parents").
- Notice how each vertical line goes through
two levels (generations or months) before it starts to branch and ..
- .. then it branches on every line after that.
This shows where our rabbits must be 2 months old to start producing their own young and
then do so every month after that.
- Notice how on each generation level, the new rabbits appear equally and optimally spaced
across the page so that there is no overcrowding at one point in the tree...
- .. and also that each horizontal branching line is the same length on each
generation and ...
- .. all are on the same side of their "parents" line in each generation and...
- ..the side they appear on swops each time, from left side to right side to left.
You can probably spot some more relationships in this Tree (for instance, that the lengths
of the horizontal branches are each 0·618 times shorter than those of the previous
generation).
1·61803 39887 49894 84820 45868 34365 63811 77203 09179 80576 ..More.. 
Continued Fraction representations
A continued fraction is a fraction of the form:
a + 1 = a + 1/( b + 1/( c + 1/( d + ... )))
b + 1
c + 1
d + ...
where a, b, c etc are integers (often only positive).
Phi is the simplest form of continued fraction since all the integers a, b, c, ... are 1.
Writing such fractions in the usual form, as above, takes a lot of space on the page, so an
abbreviation often used is to just give the integers as a list: [a,b,c,...].
a + 1 = [ a, b, c, d, ... ]
b + 1
c + 1
d + ...
In this notation
then Phi=[1,1,1,1...] which we can further abbreviate to [1] where the
numbers shown like this indicate that they are repeated in the same cycle for ever.
In some books, these periodic parts may have dots over
them in the same way that we write infinite decimal fractions such as
| . | | . | | . | | . |
| 1/3 =0·3333.. =0· | 3 |
; 1/7 = 0· | 1 | 4285 | 7 | = 0·142857142857142...;
1/12 = 0·0833333... = 0·08 | 3 |
and other authors use an overline
like this so that 1/7=0·142867.
If we have more than one integer in the repeating part, such as [6,1,5,1,5,1,5,...] we write
[6,1,5].
For more see Introduction to Continued Fractions at this site.
1·61803 39887 49894 84820 45868 34365 63811 77203 09179 80576 ..More.. 
Formulae for Phi
Phi denotes (

5+1)/2 =1·6180339... and
phi denotes (

5
-1)/2 =0·6180339... .
The basic formulae are
Phi = 1/phi = phi + 1
Phi2 = Phi + 1 and therefore
phi2 = 1 − phi.
These can be generalized and give an important and remarkable pair of results for all integers n
(positive, zero and negative):
| Phin-2 + Phin-1 = | Phin |
| phin | = phin+1 + phin+2 |
Other relationships between the powers of Phi and phi and the Fibonacci numbers that also hold for
all integer values of n are:
| Main |
= Other |
= X + Y Phi |
= A + B phi |
= C + D √5 |
| Phin |
= phi−n |
= F(n−1) + F(n) Phi |
= F(n+1) + F(n) phi |
L(n) + F(n)√5
2 |
| (−phi)n |
= (−Phi)−n |
= F(n+1) − F(n) Phi |
= F(n-1) − F(n) phi |
L(n) − F(n)√5
2 |
where L(n) is the nth Lucas number, defined
as L(n) = F(n+1) + F(n-1).
With thanks to John McNamara. There is a comprehensive list of these and other kinds of formlae on my
Fibonacci, Phi and Lucas numbers Formulae
page at this site.
Powers and Multiples of Phi Calculator
Numerical Relationships between Phi and its powers
Summarising the above, we can make a table where we relate the powers of Phi to
its multiples - and we note the Fibonacci numbers appearing again!
We can also expand the multiples of Phi using its definition as
( 5+1)/2
and find Fibonacci again. Finally, we give the continued fraction representations of these powers with the
repeating period part (if any) shown like this.
In both the
5+1)/2
and find Fibonacci again. Finally, we give the continued fraction representations of these powers with the
repeating period part (if any) shown like this.
In both the  5 forms and the continued fractions forms
we note that a new series of numbers appears -
- the Lucas numbers 2, 1, 3, 4, 7, 11, 18, 29, ... .
5 forms and the continued fractions forms
we note that a new series of numbers appears -
- the Lucas numbers 2, 1, 3, 4, 7, 11, 18, 29, ... .
Phi
power | phi
power | A + B Phi | C + D phi | Ksqrt(5)+L | decimal
value | continued
fraction |
| ... |
| Phi9 | phi−9 | 21 + 34 Phi | 55 + 34 phi | 38 + 17√5 | 76·0131556174.. | [76] |
| Phi8 | phi−8 | 13 + 21 Phi | 34 + 21 phi | (47 + 21√5)/2 | 46·9787137637.. | [46, 1, 45] |
| Phi7 | phi−7 | 8 + 13 Phi | 21 + 13 phi | (29 + 13√5)/2 | 29·0344418537.. | [29] |
| Phi6 | phi−6 | 5 + 8 Phi | 13 + 8 phi | 9 + 4√5 | 17·9442719099.. | [17, 1, 16] |
| Phi5 | phi−5 | 3 + 5 Phi | 8 + 5 phi | (11 + 5√5)/2 | 11·0901699437.. | [11] |
| Phi4 | phi−4 | 2 + 3 Phi | 5 + 3 phi | (7 + 3√5)/2 | 6·8541019662.. | [6, 1, 5] |
| Phi3 | phi−3 | 1 + 2 Phi | 3 + 2 phi | 2 + √5 | 4·2360679774.. | [4] |
| Phi2 | phi−2 | 1 + 1 Phi | 2 + 1 phi | (3 + √5)/2 | 2·6180339887.. | [2, 1] |
| Phi1 | phi−1 | 0 + 1 Phi | 1 + 1 phi | (1 + √5)/2 | 1·6180339887.. | [1] |
| Phi0 | phi0 | 1 | 1 | 1 | 1·0000000000.. | [1] |
| Phi−1 | phi1 | −1 + 1 Phi | 0 + 1 phi | (−1 + √5)/2 | 0·6180339887.. | [0, 1] |
| Phi−2 | phi2 | 2 − 1 Phi | 1 − 1 phi | (3 − √5)/2 | 0·3819660112.. | [0, 2, 1] |
| Phi−3 | phi3 | −3 + 2 Phi | −1 + 2 phi | −2 + √5 | 0·2360679774.. | [0, 4] |
| Phi−4 | phi4 | 5 − 3 Phi | 2 − 3 phi | (7 − 3√5)/2 | 0·1458980337.. | [0, 6, 1, 5] |
| Phi−5 | phi5 | −8 + 5 Phi | −3 + 5 phi | (−11 + 5√5)/2 | 0·0901699437.. | [0, 11] |
| Phi−6 | phi6 | 13 − 8 Phi | 5 − 8 phi | 9 − 4√5 | 0·0557280900.. | [0, 17, 1, 16] |
| Phi−7 | phi7 | −21 + 13 Phi | −8 + 13 phi | (−29 + 13√5)/2 | 0·0344418537.. | [0, 29] |
| Phi−8 | phi8 | 34 − 21 Phi | 13 − 21 phi | (47 − 21√5)/2 | 0·0212862362.. | [0, 46, 1, 45] |
| Phi−9 | phi9 | -55 + 34 Phi | -21 + 34 phi | -38 + 17√5 | 0·0131556174.. | [0, 76]
|
| ... |
phi = 1/Phi so the powers of phi are the negative powers of Phi.
Note that [0,a,b,c,...] is 0 + 1/(a + 1/(b + 1/(c + ...) = 1/[a,b,c, ...].
The negative powers of Phi are the positive powers of phi and are obtained by
putting a 0 at the head of the continued fraction lists above: eg
phi = 1/Phi = [0,1]
You do the maths...

- Phi3 looks as if it is just phi3+4. Perhaps this is just correct to a few
decimal places but is it really true and accurate? What other such "coincidences"
can you spot in the Table above? Almost all of them will be accurate and true
relationships, in fact.
- Try to prove some of your "coincidences" using the formulae above the table.
- What about those integers in the continued fraction forms of the powers? It looks
as if the series is
1, 3, 4, 7, 11, ..
If the next two are 18 and 29, can you spot how they are generated?
These are not the Fibonacci numbers but the pattern of generating them is similar.
The numbers are, in fact, those of a series very closely related to the Fibonacci numbers
called the Lucas numbers.
- From the table above, what do you notice about the third and fourth columns for
the following pairs of rows?
Phi and Phi-1,
Phi2 and Phi-2,
Phi3 and Phi-3,
and so on?
What if we added some of these pairs to get rid of the Phi's and subtracted the
others? What series of integers results?
 © 1996-2016 Dr Ron Knott
© 1996-2016 Dr Ron Knott

updated 25 September 2016
![]()
 If we have a brick with sides of lengths 1, Phi=1·61803...
and phi=1/Phi=0·61803... then:-
If we have a brick with sides of lengths 1, Phi=1·61803...
and phi=1/Phi=0·61803... then:-
 Another surprise awaits us when we calculate the length of the diagonal
across the brick.
Another surprise awaits us when we calculate the length of the diagonal
across the brick.![]() (12 + Phi2 +
phi2).
I'll leave you to check the algebra but the surprisingly simple answer is
(12 + Phi2 +
phi2).
I'll leave you to check the algebra but the surprisingly simple answer is
 Even more surprising is that the brick shows a simple relationship between Pi
and Phi, using the values for the diagonal D that we have just found
and the surface area S.
Even more surprising is that the brick shows a simple relationship between Pi
and Phi, using the values for the diagonal D that we have just found
and the surface area S. On a golden rectangle with sides of length phi and 1,
dividing at the golden ratio point gives two overlapping
squares whose sides are phi.
On a golden rectangle with sides of length phi and 1,
dividing at the golden ratio point gives two overlapping
squares whose sides are phi. 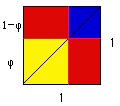
 If we take a square with sides of length 1 and divide two sides at the
golden section point, we form two new squares (yellow and blue)
and two (red) rectangles.
Notice that the diagonal is also
divided at its golden section point too.
If we take a square with sides of length 1 and divide two sides at the
golden section point, we form two new squares (yellow and blue)
and two (red) rectangles.
Notice that the diagonal is also
divided at its golden section point too. Here is a cube with sides divided at the golden section points to
split it into eight pieces.
The eight pieces are of 4 different shapes:
Here is a cube with sides divided at the golden section points to
split it into eight pieces.
The eight pieces are of 4 different shapes:
![]()
![]()
![]()
 Phi in 3 dimensions
Phi in 3 dimensions