This page contains two proofs of the formula for the Fibonacci numbers. The first is probably
the simplest known proof of the formula. The second shows how to prove it using matrices
and gives an insight (or application of) eigenvalues and eigenlines.
A simple proof that Fib(n) = (Phin – (–Phi)–n)/√5
[Adapted from Mathematical Gems 1 by R Honsberger, Mathematical Assoc of America,
1973, pages 171-172.]
Reminder:
- Phi =
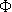 = (√5 + 1)/2
= (√5 + 1)/2
- phi =
 = (√5 – 1)/2
= (√5 – 1)/2
- Phi – phi = 1
- Phi * phi = 1
First look at the
Summary at the end of the Fascinating Facts and Figures about Phi page.
If we use -phi instead of phi, we get a single formula that covers all powers of both Phi and
-phi:
| Phi1 | = | 0 + 1 Phi | = | 1·6180339.. | and | (-phi)1 | = | 0 + 1 (-phi) | = | -0·6180339.. |
| Phi2 | = | 1 + 1 Phi | = | 2·6180339.. | and | (-phi)2 | = | 1 + 1 (-phi) | = | 0·3819660.. |
| Phi3 | = | 1 + 2 Phi | = | 4·2360679.. | and | (-phi)3 | = | 1 + 2 (-phi) | = | -0·2360679.. |
| Phi4 | = | 2 + 3 Phi | = | 6·8541019.. | and | (-phi)4 | = | 2 + 3 (-phi) | = | 0·1458980.. |
| Phi5 | = | 3 + 5 Phi | = | 11·0901699.. | and | (-phi)5 | = | 3 + 5 (-phi) | = | -0·0901699.. |
| ... |
Since Phi and -phi are the two roots of x2=x+1, we
can summarise the table above as follows:
If x2=x+1 then xn = fib(n) x + fib(n-1) for n>0.
You can either assume this is always true based on the initial examples in the table or,
you can prove it.
An easy way to prove this result is by induction, if you have covered that
method in your maths classes. I'll leave this as an exercise for you!
We can easily show that the two roots of x2=x+1 are
Phi = (1+sqrt(5))/2 = 1·6180339... and -phi = (1-sqrt(5))/2 = -0·6180339.... and thus that these
are the only two values for which their powers can be expressed as Fibonacci multiples of
themselves, as given in the formula.
So, from the formula above, we have:
| Phin = fib(n) Phi + fib(n-1) | (A) |
and also
| (-phi)n = fib(n) (-phi) + fib(n-1) | (B) |
Subtracting (B) from (A) gives:
| Phin - (-phi)n = fib(n)(Phi - (-phi)) | (C) |
and from this we derive an initial formula for fib(n):
But Phi-(-phi)=sqrt(5), so we can write this as:
To get the form of the formula which involves only Phi,
we replace phi by 1/Phi so that
The formula for fib(n) is now:
A proof using Matrices
This proof uses matrices and gives a practical application of - or introduction to -
eigenvalues and eigenlines. It is optional and only recommended for those who
have used matrices before.
All you need to know is what a matrix is and how they multiply.
Back in the Rabbits field...
Returning to Fibonacci's original rabbits problem, let's enumerate how many
mature rabbit pairs there are each month and how many immature pairs (1 month old):
month: 1 2 3 4 5
mature: 1 1 2 3 ...
young: 1 1 1 2 ...
TOTAL: 1 1 2 3 5 ...
Explanation:
The young pair are introduced into the field and are immature in month 1.
They become mature in month 2.
They give birth to a new pair in month 3.
In month 4, all those that were "young" the previous month become "mature", together
with those who were "mature" from the previous month, so the top entry is the sum of the
two entries in the column of the previous month.
The number of young in any month is just the number of pairs that were mature the
previous month, so we just copy the top entry to the bottom of the next column. These
two processes are summarized in this diagram:
month: ... n n+1 ...
mature: ... M M+Y ... the top entry is the TOTAL of the previous month
young: ... Y M ... the bottom entry is the TOP entry of the previous month
TOTAL: ... M+Y 2M+Y ...
If f(n) is the total number of pairs in month n, then it is the sum of the mature in month
n plus the young in month n. The number of mature pairs is the total of the previous month,
ie f(n-1).
The number of young is the same as the top entry of the previous month which is also
the total of the month-before-that, ie f(n-2). Hence f(n)=f(n-1)+f(n-2). Since f(1)=1, f(2)=1
then we have the Fibonacci numbers (but starting from n=1 not n=0):
month: ... n n+1 ...
mature: ... f(n-1) f(n) ...
young: ... f(n-2) f(n-1) ...
TOTAL: ... f(n) f(n+1)
We can summarise the columns as follows:
adults in month n+2: f(n+1)=f(n)+f(n-1)
young in month n+2: f(n)
or, written in matrix form:
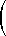 | f(n+1) | 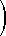 | | f(n) |
| = | 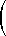 | 1 | 1 | 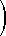 | | 1 | 0 |
| 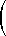 | f(n) | 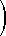 | | f(n–1) |
|
Replacing n by (n-1) in the equation above gives a matrix formula
for the vector on its right hand side.
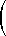 | f(n) | 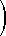 | | f(n–1) |
| = | 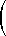 | 1 | 1 | 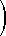 | | 1 | 0 |
| 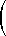 | f(n–1) | 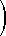 | | f(n–2) |
|
If we substitute this back in to the first formula, we have:
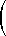 | f(n+1) | 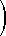 | | f(n) |
| = | 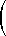 | 1 | 1 | 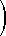 | | 1 | 0 |
| 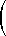 | f(n) | 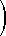 | | f(n–1) |
| = | 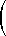 | 1 | 1 | 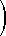 | | 1 | 0 |
| 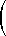 | 1 | 1 | 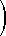 | | 1 | 0 |
| 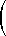 | f(n–1) | 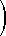 | | f(n–2) |
| = | | |
We can keep on doing this, each time getting ahigher power of the 2-by-2 matrix
until eventually we get right back to the original month 0 and month 1 (i.e.
the unit vector):
You will see that we have called the matrix M.
We need to find its n-th power if
we are to determine f(n+1) and f(n). Raising a matrix
to the n-th power is a lot of work! Fortunately, matrix algebra
comes to the rescue and provides a quick way of evaluating it with very little work.
What is a formula for the n-th power of this matrix?
If we can find a formula for the n-th power of M, we have a formula for f(n).
There is a useful method that applies to matrices to find such a formula.
If we can write matrix M as the product of 3 matrices: Q D Q-1,
where D is a matrix whose only
entries are on its main diagonal, then Mn is
Mn = (Q D Q-1)(Q D Q-1)...(Q D Q-1)
All the Q.Q-1 terms nicely cancel out so we get
Mn = Q Dn Q-1
What is the advantage of the new form - we still need to find Dn?
The answer is that since D is in diagonal form then its powers are easy to work out:
Eigenvalues
The entries we need for D are the eigenvalues of M, found by solving this equation:
| 0 = det | 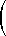 | 1–k | 1 | 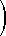 | | 1 | 0–k |
| = | (1–k)(0–k) – 1 1 = k2 – k – 1 1 = k2 – k – 1 |
There are two values for k, k=Phi and k=–phi.
So the D matrix can be
What about Q?
Now we've found D as a matrix in diagonal form, what about Q? This is defined by the
eigenlines of our original matrix M, that is, for eigenvalues a and b ( ours were a=Phi and
b=-1/Phi ) we want to solve:
| ( | 1 1
1 0 | )( | x
y | ) | = | ( | ax
ay | ) |
|
( | 1 1
1 0 | )( | x
y | ) | = | ( | bx
by | ) |
giving y=x/a and y=x/b. From this we can "invent" a matrix Q as follows:
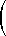 | 1 | 1 | 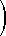 |
| 1/a | 1/b |
Its determinant is (a-b)/ab which is just -sqrt(5) for our values of a and b so we can form
the inverse of Q:
| Q–1 = |
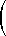 | a/√5 | 1/√5 | 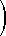 |
| –b/√5 | –1/√5 |
Now we can write our matrix M in the Q D Q-1 form:
So we have
Looking back, we had:
Now we replace Mn by Q Dn Q-1 and multiply out the matrices:
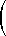 | f(n+1) | 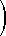 | | f(n) |
|
= |
|
| = | | 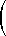 | an | 0 | 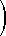 | | 0 | bn |
| | 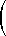 | 1 | 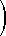 | | 0 |
| = | |
So the vector on the left is equal to the vector on the right. Both top and bottom components give
the same formula, but the top has (n+1) in place of the n in the bottom one.
Finally, then, we have it - our formula for f(n):
| f(n) = | an – bn | where a = Phi = 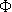 = = | 1+ 5 5 | and b = –phi = –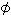 = = | 1– 5 5 |
 |  |  |

 |  | | 5 |
| 
2 | 
2 |
See also:
 A Primer on the Fibonacci Sequence - Part II by S L Basin, V E Hoggatt Jr in
Fibonacci Quarterly vol 1, pages 61 - 68 for more examples of how to derive
Fibonacci formulae using matrices.
A Primer on the Fibonacci Sequence - Part II by S L Basin, V E Hoggatt Jr in
Fibonacci Quarterly vol 1, pages 61 - 68 for more examples of how to derive
Fibonacci formulae using matrices.
WHERE TO NOW???
 Fibonacci Home Page
Fibonacci Home Page
 Return to
A Formula for the Fibonacci Numbers
Return to
A Formula for the Fibonacci Numbers
 © 1996-2003 Dr Ron Knott
© 1996-2003 Dr Ron Knott

updated 30 October 2003



![]() A Primer on the Fibonacci Sequence - Part II by S L Basin, V E Hoggatt Jr in
Fibonacci Quarterly vol 1, pages 61 - 68 for more examples of how to derive
Fibonacci formulae using matrices.
A Primer on the Fibonacci Sequence - Part II by S L Basin, V E Hoggatt Jr in
Fibonacci Quarterly vol 1, pages 61 - 68 for more examples of how to derive
Fibonacci formulae using matrices.
 Return to
A Formula for the Fibonacci Numbers
Return to
A Formula for the Fibonacci Numbers