Here's an example of why the Fibonacci numbers are the answer

What is the Fibonacci series?

One way to explain that the Fibonacci series is the correct answer is to show that the problem satisfies the three conditions of the Fibonacci (Recursive) Definition:

• f(n) = f(n-1) + f(n-2)

On its own, the formula above is satisifed by many series that are not "the" Fibonacci numbers because we have not given any starting numbers.
For example, we could start with two 2's as the first pair in the series and then apply the formula above to get 2+2=4 as the next, (the series is now 2,2,4) and then 2+4=6 as the next one (the series is now 2,2,4,6) as so on to get:
2,2,4,6,10,16,26,42,...
[In fact, this particular series is closely related the "the" Fibonacci series 0,1,1,2,3,5,8,... - can you spot that relationship?]

So we will need starting values as well as the formula above.

For "the" Fibonacci numbers, we could start with
• 0 and 1 to get: 0, 1, 1, 2, 3, 5, 8, 13, ... or
• 1 and 1 to get: 1, 1, 2, 3, 5, 8, 13, 21, ... or
• 1 and 2 to get: 1, 2, 3, 5, 8, 13, 21, 34, ... or
• 2 and 3 ...
• ...

• The general case:
  the number of solutions to the problem of size n can be explained as the number of solutions to the problem of size (n-1) PLUS the number of solutions of the problem of size (n-2), i.e.
  if f(n) is "the number of solutions to the problem of size n" then f(n) = f(n-1) + f(n-2)
  This is called the general case because it must apply for all sizes, n, of the puzzle.
• The starting cases:
  We need to show that the number of solutions to TWO particular small problems (e.g. of size n=1 and size n=2) are 0 and 1, or 1 and 1, or 1 and 2, or 2 and 3 etc.

The Brick Wall Puzzle

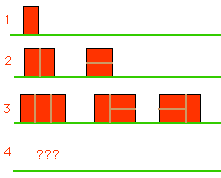
For this puzzle, f(n) means "the number of patterns for walls of height 2 and length n" and the solutions we have at present are

Two starting cases Usually it is quite easy to verify the STARTING CASES for a puzzle because we can find all the solutions and just count them.
For this puzzle we can show that f(1)=1 and that f(2)=2 as follows, using the picture of the solutions above:

f(1)=1

There is just one pattern for a wall of length 1 (the single brick is placed upright), so f(1)=1.

f(2)=2

There are 2 patterns if we have a wall of length 2 as we have seen in the diagrams of the puzzle page, so f(2)=2 "the number of patterns for walls of height 2 and length 2 is 2".

Now for the general case: f(n)=f(n-1)+f(n-2)

What about f(n) - the number of patterns for walls of height 2 and length n?
This is the general case and we must be sure that our reasoning applies to ALL n bigger than 1 (we have covered the two cases for not bigger than 1 above).

Consider what happens at the left end of the wall....

.... either there is a brick on its end
....or else there is a brick on its side - in which case there must be another one on top of it as there is no other way to make the height of 2.

There are no more cases and these two cases cover all possible ways of starting a wall of length bigger than 1.
Let's look at these two cases:

• If we start a wall of length n with a single upright brick then we need patterns for walls of length n-1 to complete it. How many of these are there? There are f(n-1) of them since that's what f(n-1) means.
• The only other way a pattern of length n can be made is to start with the two-flat-bricks-on-top-of-each-other pattern. We can then continue with any wall pattern of height 2 and of length n-2 and there are f(n-2) of these.

So all the ways of finding walls of length n are covered by the two cases:
an upright brick first and then any pattern of length n-1
or else the two-flat-bricks followed by any pattern of length n-2.

So the number of patterns of length n is the sum of the number of patterns of length (n-1) and the number of patterns of length (n-2). In terms of the "f" notation in mathematics, we have

f(n) = f(n-1) + f(n-2) generally

So BOTH conditions are fulfilled:
• the general case:
  f(n) = f(n-1) + f(n-2) generally
• and the two starting cases:
  f(1) = 1 and f(2) = 2

With thanks to Mats Lofkvist for helping make this page more accurate.

© 1996-2006 Dr Ron Knott
updated: 13 February 2001