|
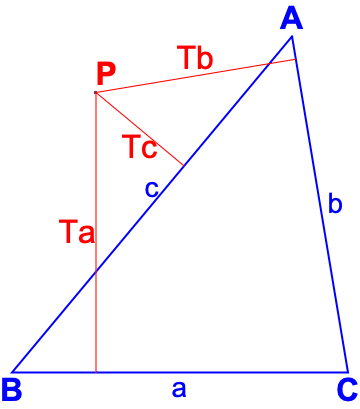
The 3 distances of a point from each of the sides of the triangle.
If point P is (signed) distance Ta from side BC, Tb from side AC and Tc from side AB then its exact
trilinear coordinates are written as Ta:Tb:Tc. A point on the same side of BC as vertex A has positive distance, 0 if on the line and a negative distance if on the other side of that line; similarly for the other sides. So in the diagram here, Ta and Tb are positive and Tc is negative.
|
|
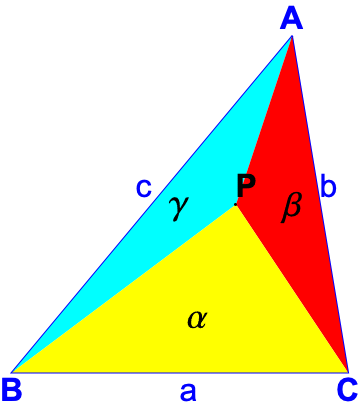
A point P is represented by the signed areas of the three sub-triangles made by joining P to
vertices A, B and C, called the exact barycentric coordinates and
written as {area of PBC, area of PAC, area of PBA} often written as {α, β, γ} .
|
Similarly, there are points whose trilinears when converted to barycentrics sum to 0.
The normalized barycentric coordinates for these points have a maximum absolute coordinate value equal to 1.
The ETC centers X(30) and X(511) through to X(519) are examples.
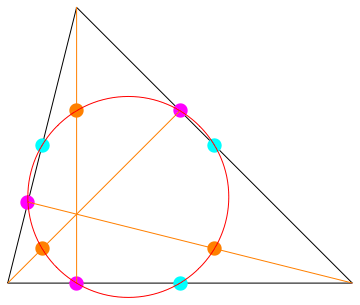
 The following 9 points all lie on the same circle:
The following 9 points all lie on the same circle:
- The foot of each altitude the point on a side where a line perpendicular to that side goes through the other vertex
Trilinears 0:cos(C):cos(B), cos(C):0:cos(A), cos(B):cos(A):0 - the mid-points of the sides
Trilinears: 0:1:1, 1:0:1, 1:1:0 - the mid-point of the lines from the orthocentre to the vertices
Its radius is one half of the circumcircle through all 3 vertices.
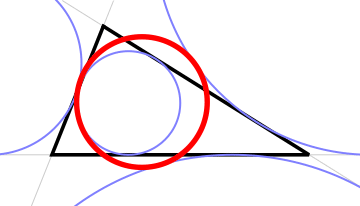
Feuerbach's Theorem of 1822 states that the nine-point circle is tangent to the incircle and the three excircles.
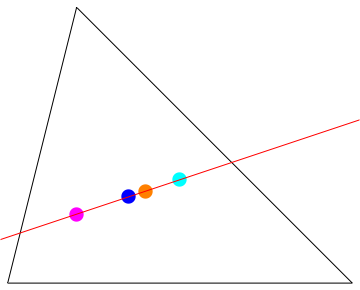 The following points are on the same line:
The following points are on the same line:
- the centroid where the lines joining a vertex to the mid-point of the side opposite all meet
Barycentrics {1,1,1} - the circumcentre of the circle through all 3 vertices
Trilinears cos(A):cos(B):cos(C) - the orthocentre where the three altitudes meet
Barycentrics {tan(A),tan(B),tan(C)} - the 9-point centre Trilinears cos(B-C):cos(C-A):cos(A-B)
Many other ETC centers lie on the Euler line. A list is given on Eric W Weisstein's "Euler Line" Mathworld page
- see Links and References at the foot of this page.