
Easier Fibonacci puzzles
All these puzzles except one (which??) have the Fibonacci numbers as their answers.
So now you have the puzzle and the answer - so what's left? Just the explanation of
why the Fibonacci numbers are the answer - that's the real puzzle!!
Puzzles on this page have fairly straight-forward
and simple explanations as to why their solution involves the Fibonacci numbers;.
Puzzles on the next page are harder
to explain but they
still have the Fibonacci Numbers as their solutions.
So does a simple explanation exist for any of them?
Contents of this Page
Puzzles that are simply related to the Fibonacci numbers....
Building puzzles
Seating arrangements
Finding paths
Coin puzzles
Miscellaneous puzzles
Make up your own puzzle...
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ..More.. 
If we want to build a brick wall out of the usual size of brick
which has a length twice as long as its height, and if our wall
is to be two units tall, we can make our wall in a number of patterns,
depending on how long we want it:
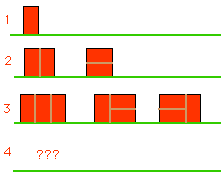 There's just one wall pattern which is 1 unit wide - made by putting the brick on its end.
There's just one wall pattern which is 1 unit wide - made by putting the brick on its end.
There are 2 patterns for a wall of length 2: two side-ways bricks laid on top of
each other and two bricks long-ways up put next to each other.
There are three patterns for walls of length 3.
How many patterns can you find for a wall of length 4?
How may different patterns are there for a wall of length 5?
Look at the number of patterns you have found for a
wall of length 1, 2, 3, 4 and 5. Does anything seem familiar?
Can you find a reason for this?
Show me an example of why the Fibonacci numbers are the answer
Variation - use Dominoes
A domino is formed from two squares. In this variation of the Brick Wall puzzle,
we are not interested in the spots on the dominoes, just their shape. If you like,
turn the dominoes over with the spots underneath so that they all look the same.
Start by placing n dominoes flat on a table, face down,
and turn them so that all are in the "tall" or "8" position
(as opposed to the "wide" or "oo" orientation). Pack
them neatly together to make a rectangle which is as long as you like but only 2 squares tall.
Take the same number of dominoes and, using this rectangle as the picture
to aim at in a jigsaw puzzle, see
how many other flat patterns you can make which have exactly this shape.
This time dominoes can be placed in either the tall or wide direction in your design.
Make a table of the patterns you have found and the number of patterns possible
using 1 domino (easy!), 2 dominoes, 3 dominoes, and so on,
not forgetting to include the original rectangle design too.
In mathematics, this is called tiling problem using dominoes and we wish to tile an
area 2xn.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ..More.. 
This puzzle was suggested by Paul Dixon, a mathematics teacher at
Coulby Newham School, Middlesborough.
A new estate of houses is to be built on one side of a street - let's
call it Leonardo's Lane. The houses are to be of two types:
a single house (a detached house) or
two houses joined by a common wall (called "a pair of
semi-detached houses"
in the UK) which take up twice the frontage on the lane as a single
house.
For instance, if just 3 houses could be fitted on to the plot of land
in a row,
we could suggest:
 |
DDD: Three detached houses |
|
SD: a pair of semi's first followed by a detached house |
|
DS: a detached house followed by a pair of semi's |
If you were the architect and there was space for
just n dwellings on the Lane of just the two kinds mentioned
above, what combinations could you use along the lane?
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ..More.. 
[Suggested by Dmitry Portnoy (7th grade)]
A boat building company makes two kinds of boat:
a canoe, which takes a month to make and
a sailing dinghy and they two months to build.
The company only has enough space to build one boat at a time but it does have plenty of customers
waiting for a boat to be built.
Suppose the area where the boats are built has to be closed for maintenance soon:
- if it is closed after one more months work, the builders can only build one boat
- a canoe - before then. Let's write this plan as C;
- if it is to be closed after 2 months work, it can EITHER build 2 canoes (CC)
OR ELSE build one dinghy (D),
so there are two plans to choose from;
- if it closed in three months time, it could make 3 canoes (CCC) or a dinghy followed by a
canoe (DC) or a canoe and then a dinghy (CD); so there are three choices of plan.
- What choices are there if it closed after 4 months?
- ... or after 5 months?
- ... or after n months?
You can adapt this puzzle:
- .. to larger boats: patrol boats taking a year to build or container ships which take two years
to make
- .. or you can make the problem smaller, and consider model boats, a small kit taking
one month on your desk or a larger kit taking two months.
How many more ideas can you come up with for a similar puzzle?
Ones and Twos
Aphrodite and Rodney are playing with coloured rods. There are lots of each of the various lengths,
each length having its own unique colour, from
single orange ones
(length 1 which are cubes), length 2 are magenta,
length 3 are blue and so on as shown in this table:
| length 1 | |
| length 2 | |
| length 3 | |
| length 4 | |
| length 5 | |
| ... | ... |
How many coloured patterns are there making a line of total
length N if the only rods available are of lengths 1 and 2?
For instance, there are 3 ways to make a line 3 units long:
The first two are different because the order of the colours is different.
It's Fibonacci to the rescue again, but why?
Some stepping stones cross a small river. How many ways back to the bank are there
if you are standing on the n-th stone? You can either step on to the next stone
or else hop over one stone to land on the next.
If you are on stone number 1, you can only step (s) on to the bank: 1 route.
If you are on stone 2, you can either step on to stone 1 and then the bank (step, step or ss)
OR you can hop directly onto the bank (h):
| | | step | | step | | ss |
|  | |  | |  |
 |
 |
| | | ----- hop ----> | | h |
|  | | 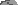 | |  |
 |
 |
| 2 sequences |
From stone 3, you can step, step, step (sss)
or else hop over stone 2 and then step (hs)
or else step on to stone 2 and then hop over stone 1 to the bank (sh):
| | | step | | step | | step | | sss |
| 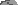 | | 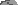 | | 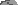 | |  |
 |
 |
| | | ----- hop ----> | | step | | hs |
| 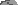 | | 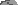 | | 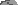 | |  |
 |
 |
| | | step | | ----- hop ----> | | sh |
| 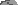 | | 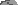 | | 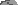 | |  |
 |
 |
| 3 sequences |
Why are the Fibonacci numbers appearing?
[With thanks to Michael West for bringing this puzzle to my attention.]
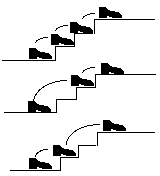
I try and take the stairs rather than the elevator whenever I can so that
I get a little more exercise these days. If I'm in a hurry, I can leap two stairs
at once otherwise it's the usual one stair at a time. If I mix these two kinds of
action - step onto the next or else leap
over the next onto the following one -
then in how many different ways can I get up a flight of n steps?
For example, for 3 stairs, I can go
 1: step-step-step
1: step-step-step
or else
2: leap-step
or finally
3: step-leap
...a total of 3 ways to climb 3 steps.
How many ways are there to climb a set of 4 stairs? 5 stairs? n stairs? Why?
Adapted from the 1995 third edition (example 2, pages 280-281) of
 Applied Combinatorics (4th Edition) by A Tucker, Wiley, 2001, 464 pages.
Applied Combinatorics (4th Edition) by A Tucker, Wiley, 2001, 464 pages.
In mathematics, Leonardo's Lane, Boat Building, Ones and Twos, Stepping Stones and Leonardo's Leaps
are essentially the same problem:
find a sum totalling n using only 1s and 2s.
Since we may have any number of 1s and of 2s, and the order of them in the sum matters, each solution is
called a
composition of n with parts {1,2}
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ..More.. 
No one!
As in the last problem with rods, Aphrodite is again playing with her coloured rods
this time with Rodrigo.
Rodrigo has just taken out all the length
1 rods (the orange cubes) to play with and has left her with all the rest. She can always make a line of
length n because there is a variety of coloured rod of that length available, provided n is not one, of course!
So the puzzle is:
In how many ways can she make a line of length N if there are
no rods of length 1 available?
| length 2 | |
| length 3 | |
| length 4 | |
| length 5 | |
| ... | ... |
|
|
|
|
For a line of length 2 there is only a rod of length 2 |
2 |
|
For a line of length 3, she can use only a rod of length 3.
|
|
3 |
|
|
But for a line of length 4, she can use either a rod of length 4 |
4 |
|
| or else two rods of length 2. |
2 + 2 |
|
| When it comes to making a line of length 5: one rod of length 5 |
|
5 |
| a rod of length 3 followed by one of length 2: |
| 3 + 2 |
| or she could put the rod of length 2 first and the 3-rod after it: |
|
2 + 3 |
|
The solutions are summarized on the right, as sums.
So what we are doing is listing sums where the number ONE must not appear in the sum. The order of the numbers
matters so that 2+3 is not the same sum as 3+2 in this problem.
In mathematics, this is called the problem of finding a
composition of n which does not contain 1.
The Belgian schoolteacher Georges Cuisenaire (1891-1976) invented these small square rods
of integer lengths to help primary school
and kindergarten students develop their understanding of whole numbers and arithemtic.
The colours used on this page do not correspond to Cuisenaire's rod colours.
Parcelling Boxes
A set of square boxes is to be mailed as one parcel. As the person in the post room you
have the job of sealing them round the outside with parcel tape (sticky tape).
A single square box has to have
its four sides taped round but the front and back of every box has no tape -
they have information
about the address and sender etc.
The square boxes are always parcelled as a single layer so we can represent them as squares
and the total number of lines on the outside tells us the number of sides that must be taped
(the number of sides on the perimeter of the parcel). Of course the boxes are close-packed and have no
"holes" in their arrangement.
The only condition for making a parcel is that the boxes stack so that each layer/row of boxes
(the boxes at the same height above the base) never has more boxes than the layer below it.
|
This condition rules out these parcels with a row of 2 boxes stacked above a single box at the base:
| 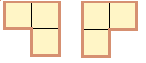 |
Count all the possible arrangements of boxes according to the length of
sticky tape used (that is, the number of sides on the perimeter of the shape).
number of
sides on
perimeter | parcel shapes | number of
parcels |
|---|
| 4 | ![[][]](boxes4.gif) | 1 |
| 6 | ![[||]](boxes6.gif) | 2 |
| 8 | ![[||]](boxes8.gif) | 5 |
| 10 | ? | 13 |
| ... | ... | ... |
If the answers in the final column are the Fibonacci numbers, where is 3?
See if you can spot how the answers are related to the Fibonacci numbers here.
 Inspired by
How the odd terms in the Fibonacci Sequence stack up S Rinaldi, D G Rogers, Mathematical Gazette
(2006) pages 431-442 available in
PDF format.
Inspired by
How the odd terms in the Fibonacci Sequence stack up S Rinaldi, D G Rogers, Mathematical Gazette
(2006) pages 431-442 available in
PDF format.
In mathematics this is another example of a tiling problem. We want the perimeter of a collection of connected
squares (with no holes).
Sprouting Sea-weed
In this puzzle we look at the shapes of a sprouting sea-weed anchored to the sea floor.
The sea-weed in this puzzle can sprout a new frond (segment) only from a single growing point
or, at the top of the plant, we can make a new growing point but there is
only ever one point in the plant from which a new frond can grow
as follows:
|
The topmost layer of fronds all grow from a
single growing point at their base, shown here as a red dot. We can grow another frond to add to those at the
growing point.
It is the number of fronds that matter on the topmost level not where the new one
is placed among them.
|
We can move the growing point from the bottom to the top of any one of the topmost fronds.
All the fronds are different so the tips of any of the topmost fronds can be the new growing point
making differently shaped sea-weeds.
|

|

|
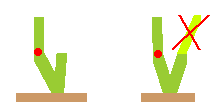
| So once the growing point has moved up to the top of a frond,
it can't "jump" and grow a new frond on a neighbour! |
How many shapes of sea-weed can you find that consist of n fronds?
In the table of shapes here, the new cell that has grown is shown in the lighter green.
number of
fronds | sea-weed shapes | number of
shapes |
|---|
| 1 |  | 1 |
| 2 | 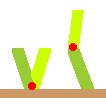 | 2 |
| 3 |  | 5 |
| 4 | ? | 13 |
| ... | ... | ... |
If the answers in the final column are the Fibonacci numbers, where is 3?
See if you can spot how the answers are related to the Fibonacci numbers here.
 Inspired by
How the odd terms in the Fibonacci Sequence stack up S Rinaldi, D G Rogers, Mathematical Gazette
(2006) pages 431-442.
Inspired by
How the odd terms in the Fibonacci Sequence stack up S Rinaldi, D G Rogers, Mathematical Gazette
(2006) pages 431-442.
In mathematics, this is called a tree-counting problem. The trees are rooted.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ..More.. 
Chairs in a row: The Teachers version
This time we have n chairs in a row and a roomful of people.
If you've ever been to a gathering where there are teachers present, you will know
they always talk about their school/college (boring!). So
we will insist that no two teachers should sit next to each other
along a row of seats and count how many ways we can seat n people,
if some are teachers  (who cannot be next to each other) and
some are not
(who cannot be next to each other) and
some are not  . The number of seating arrangements is always a Fibonacci number:
. The number of seating arrangements is always a Fibonacci number:
|
1 chair |  or or  | 2 ways |
| 2 chairs |   or or   or or   | 3 ways |
| since we do not allow   |
| 3 chairs |    , ,    , ,    , ,    or or    | 5 ways |
| this time    , ,    and and    are not allowed. are not allowed. |
You can write the sequences using T for Teacher and N for Normal people - oops - I mean Not-a-teacher !!
There will always be a Fibonacci number of sequences for a given number of chairs, if no two teachers  are allowed to sit next to each other!
are allowed to sit next to each other!
In mathematics, this is the problem of enumeration (counting) binary strings (sequences of 1s and 0s) where there are no
two consecutive 1s (a 1 representing a teacher, and a 0 for each other person).
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ..More.. 
Chairs in a Row: The Friendly Version
This variation is a little friendlier to teachers.
Everyone, teacher  or not
or not  , must not sit
on their own, but a teacher
, must not sit
on their own, but a teacher  must be next to another teacher
must be next to another teacher  and a non-teacher
and a non-teacher  must be
next to a non-teacher
must be
next to a non-teacher  .
.
So we can have
... 

 ...
since the two teachers have the other teacher next to them.
The non-teacher on the right of these 3 will now also need another non-teacher on his other side
so that he too is not left on his own.
...
since the two teachers have the other teacher next to them.
The non-teacher on the right of these 3 will now also need another non-teacher on his other side
so that he too is not left on his own.
A special extracondition in this puzzle
is that any seating arrangement must also start with a teacher!
| 1 chair: | - | 0 ways |
| 2 chairs: |   | 1 way |
| 3 chairs: |    | 1 way |
| 4 chairs: |     or or     | 2 ways |
| 5 chairs: |      or or      or or      | 3 ways |
There will always be a Fibonacci number of arrangements if we start with a teacher.
What happens if we start with a non-teacher always?
What happens if we have no restriction on the first seat?
The answers to these two questions also involve the Fibonacci numbers too!!
In mathematics, this is the problem of enumeration (counting) binary strings (sequences of 1s and 0s) where there are no
single bits, that is each bit must be next to an equal bit on at least one side of it.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ..More.. 
Chairs in a Row: The Singles Version!
This time we have the antisocial version which we may also perhaps call the Singles version or the British version!
As you know, some British people can be very reserved sometimes and
like not to bother people by sitting next to them in public places if they can possibly help it.
So this time we still consider rows of seats of different lengths, as before,
but this time insist that no one can sit next to anyone else!
There may be no one in the row, or just one person, but wherever there are two people or more,
they must always be separated by at least one empty seat so that no one sits next to anyone else.
| Here is a row of 1 seat which is empty: |
|
|
and a row of 1 seat which is occupied: |
|
so there are 2 ways to fill a row of 1 seat in this puzzle.
|
What about a row of 2 seats:
so there are 3 ways to fill this row.
|
For a row of 3 seats we have:
|
What about 4 seats in a row? and 5?
 See Antisocial Dinner Parties by R Lewis in
Fibonacci Quarterly 1995, vol 33, pages 368-370.
See Antisocial Dinner Parties by R Lewis in
Fibonacci Quarterly 1995, vol 33, pages 368-370.
In mathematics, this is another binary-string enumeration problem, where the sequences of 1s and 0s
(1 for a person, 0 for an empty seat) is prohibited if it contains 11 anywhere in it.
Chairs in a Row: the Couples version 
In this version, we have a row of n chairs. People arrive in twos and want to sit next to their partner.
How many ways can a row of n chairs be filled with couples or be left empty?
For instance, a row of 4 chairs can be filled in the following 5 ways:
Notice that the first case is all chairs empty.
How many are there for a row of 5 chairs?
And what about a row of 2 or 3 chairs?
In mathematics, this is the problem of enumeration (counting) binary strings (sequences of 1s and 0s) where there are always an even number
of consecutive 1s.
Chess Match Seating 
I am arranging a chess match at my local chess club. The seating will be in two rows so that
people can wander around the outside of the players' area and watch any game they like but they are not permitted
between and among the players to minimize any distraction.
In order to give an
element of randomness to who plays whom, the players will seat themselves anywhere they like
in the two rows and, when they are all seated, then I will place chess boards between neighbouring pairs
of players. Of course I want to ensure that when I do this there are no players left isolated on their own as they are not
permitted to move once seated.
So given two rows of n players (2n in total) to play
n games at the same time,
how many ways are there for me to place the n chess boards between neighbouring pairs of players
so the everyone is playing a game?
Here are the 3 ways to orient 6 players ( )
sitting on opposite sides of 3 chessboards (
)
sitting on opposite sides of 3 chessboards ( ):
):
note that the players seats are fixed in the room:
It is clearly always possible to place the boards no matter how long the rows are can put all
the boards between a player in the top row and the corresponding player in the bottom row.
But how many was are there altogether if there for 4 games (8 players)? 5 games (10 players)?
n games (2n players)?
In mathematics, this is the problem of matchings (finding pairs of points) on a network of possible connections which is formed from 2
copies of a Path graph P(n), corresponding points joined (or P(2)×P(n)) and we wish all points to be matched with just one other
using the connections (edges) of the graph.
When all the points are so paired, it is called a
Perfect Matching.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ..More.. 
Here is a picture of a bee starting at the end of some cells in its hive.
It can start at either cell 1 or cell 2 and moves only to the right
(that is, only to a cell with a higher number in it).
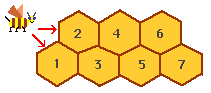
There is only one path to cell 1, but
two ways to reach cell 2: directly or via cell 1.
For cell 3, it can go 123, 13, or 23, that is, there are three different paths.
How many paths are there from the start to cell number n?
The answer is again the Fibonacci numbers.
Can you explain why?
In mathematics, this is a problem of finding all paths on part of a triangular network (the nodes have
two or three edges meeting at them).
Fibonacci's Ravenous Rabbit and the Two Lettuce Rows 
On an earlier page we met Fibonacci's rabbits. But Fibonacci
neglected to say how those rabbits found their food
and recently I found out!
I had planted out two long rows of lettuces but found fairly soon that overnight a rabbit had
discovered my new juicy salad plants and had eaten its way through some of them, leaving a
tell-tale trail of paw-prints!
After replacing the eaten ones it returned and the same thing happened.
Watching the trails over several days,
I noticed my nocturnal visitor seemed to follow the same pattern in its nightly rampages through my lettuce patch:-
- The field of rabbits was off to the top left, so my hungry rabbit
always started each night's forage at the top left lettuce
- it must have smelled the lettuces stretching out before it because it
always moved along a row to the right and never went back on itself to the left
- it changed row at random, always moving to the nearest on the other row,
straight down or up
- it never passed over a lettuce without eating the whole of it!
So, if you are one of Fibonacci's filching and ravenous rabbits,
paws  for thought
and let us ("lettuce"
for thought
and let us ("lettuce"  )
see if you can find the answer to this question:
)
see if you can find the answer to this question:
how many paths of n lettuces can you find through my lettuce patch?
List your paths by the number of lettuces that were eaten on that night.
For instance, here are the three paths through my lettuce patch where the rabbit has eaten
3 of my lettuces:
Notice that in the middle path, the rabbit can now only go along the bottom row to the next lettuce on its right
but in the first and last it can proceed either by changing row or continuing on the same row.
How many paths are there if it eats 4 lettuce? How many for 5? 6? ...
 Inspired by
Self-avoiding walks and Fibonacci Numbers Arthur T Benjamin Fibonacci Quarterly (2006), pages 330-334.
Inspired by
Self-avoiding walks and Fibonacci Numbers Arthur T Benjamin Fibonacci Quarterly (2006), pages 330-334.
In mathematics, this is the problem of finding a certain kind of path in a
lattice (a rectangular collection of lines around squares)
and hence the pun on
lettuce 
.
[Thanks to Art Benjamin for that one!]
- Problem B-180: Directed lines from (0,0) to (n,0) Reuben C. Drake, Fibonacci Quarterly vol 8.1 (1970) page 106
The solution is given in:
- Bunny Paths? Fibonacci Quarterly, vol 8.5 (1970) page 547
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ..More.. 
Perhaps, like me, when using a coin to make a decision, you have said
"Heads I win, Tails you lose"!!
This puzzle is about coin tossing, and in particular about how long we might have to wait before we get
two heads, one after the other.
If we toss a coin twice, then there are four possible outcomes:
In only 1 of these four do we get two heads.
What happens if we have
to wait for exactly three tosses before we get two heads?
This time the possibilities are
TTT, TTH, THT, HTH, HTT, THH
Note that we do not have HHT or HHH in this list because we would
have had two heads after only 2 tosses which was covered earlier. So there is
again just 1
way to get two heads appearing at the end of three tosses,
H on the second and H on the third toss.
How many ways are there if HH appears
on the 3rd-and-4th tosses?
TTTT, TTTH, TTHT, TTHH, THTT, THTH, HTHH, HTHT, HTTH, HTTT.
This time we find 2 sequences.
Can you find a method of generating all the sequences of n coin-tosses
that do not have HH until the last two tosses?
Can you find a formula for
how many of these will end in HH?
OPTIONAL EXTRA!!!
What about the number of sequences of n coin tosses that end with
three Heads together?
Does this have any relationship to the Fibonacci numbers?
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ..More.. 
Some countries have coins or notes of value 1 and 2. For instance,
in Britain
we have coins with values 1 penny (1p) and 2 pence (2p) as well as
1 pound (£1) and 2 pounds (£2).
The USA has 1 cent (1¢) and 5 cent (5¢) coins and
no 2 cents coin, but it does have ten dollar ($10) and twenty dollar ($20)
paper notes (bills).
This problem uses coins or notes of values 1 and 2.
Imagine, if you like, that you
are buying a ticket to park your car in a UK city centre car park
from a ticket machine that takes only £1 and
£2 coins and that it costs £1 per hour to park.
If we have only £1 and £2 coins, in how many ways can we
insert coins to buy a ticket with just these two types of coin?
For instance, if "+" means followed by, we have:-
Price
£ | Coin orders | Number of
solutions |
|---|
| 1 | 1 | one way |
| 2 | 1+1
2 | two ways |
| 3 | 1+1+1
1+2
2+1 | three ways |
Since we are counting the number of different ways of inserting coins
into the ticket machine to make a fixed value,
then 1 followed by 2 is not the same as
2 followed by 1.
You will have guessed how many ways there
are to make up £4 and the general answer by now, but check it out and find all 5
ways of inserting 1's and 2's to make a total of 4!
The challenge is: can you explain why the Fibonacci numbers appear
yet again?
Variation: You are putting stamps on a parcel to make a value of
10 pence but all you have are some 1p and 2p stamps. The stamps are placed in
a single row at the top of the parcel.
Follow up: What if we are interested in collections of coins rather than
sequences?
Here 1p+2p is the same collection as 2p+1p since they both contain the
same number of each type of coin.
Mathematicians call a collection that sums to n
a partition of n. They have many
applications in mathematics.
Can you find a simple link between answers to the Change puzzle and your answers to the
Stepping Stones puzzle?
In mathematics, this is a problem of finding the number of combinations of numbers with the same sum.
If we were interested in just the collection (of coins) as a whole so that
1+2+1, 1+1+2 and 2+1+1 are the same since all contain a single 2 and two 1s, then we are counting partitions of an integer.
In this puzzle, it is combinations that we are counting,
but we only allow the use of 1s and 2s and no higher numbers in the sums, so they are restricted combinations.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ..More.. 
This problem is about the best way to pass on news to lots of people using the telephone.
We could just phone everyone ourselves, so 14 people to share the news with
would take 14 separate calls.
Suppose each call takes just 1 minute, then we will be on the phone at least 14 minutes
(if everyone answers their phone immediately).
Can we do better than this?
We could use the speakers on the phone - the "hands free" facility which puts
the sound out on a speaker rather than through the handset so that others in the
room can hear the call too. For the sake of a puzzle,
let's suppose that 2 people hear each call.
That would halve the number of calls I need to make. My 14 calls now reduces to 7.
Can we do better still?
Well, we could ask each person who receives a call to not only put the call through the loudspeakers
but also to do some phoning too.
So if two people hear the message, they could each phone two others and pass it on
in the same way and so on. Here's what it looks like if I have 14 people to phone
in this system as the calls "cascade". In the first minute, my first call is heard by
A and B. A's call is heard by both C and D; B's call by E and F, and so on as
in this diagram:
me
-------------^-----------
first minute A B
-----^----- ------^-----
second minute C D E F
---^--- ---^--- ---^--- ---^---
third minute G H I J K L M N
So all 14 people have heard the news in only 3 minutes!
[This is an example of recursion - applying the same optimising principle at all
levels of a problem.]
Can we do even better than this?
Yes - if all the people got together in one room, it would only take one minute!
So let's assume that I cannot get everyone together and I have to use the phone.
Now here is your puzzle. The phones in my company are rather old and do not have an
external speaker (and no "conference call" facility) - only one person can hear each call.
So I decide that I will phone only two people using two separate calls.
I shall give them the news and then ask that they do the same and phone just two
more people only. What is the shortest time that the news can pass to 14 people?
- Draw the cascade tree of telephone calls, or the telephone tree
for this problem. It begins like this:
me
-------------^-----------
first minute A |
-----^-------- |
second minute C | B
---^----- | ---^---
third minute D | E F |
---^-- | ---^--- ---^--- |
... ... ... ... ... ... ... ...
How does the tree continue?
- What is the maximum number of people in the office that
could hear the news within N minutes using this method?
Why is the answer related to the Fibonacci numbers?
 Inspired by Joan Reinthaler's
Discrete Mathematics is Already in the Classroom - But It's Hiding pages 295-299 in:
Inspired by Joan Reinthaler's
Discrete Mathematics is Already in the Classroom - But It's Hiding pages 295-299 in:
 Discrete Mathematics in Schools,
DIMACS Series in
Discrete Mathematics and Theoretical Computer Science, Volume 36,
American Mathematical Society 1997.
This is a great book!
Discrete Mathematics in Schools,
DIMACS Series in
Discrete Mathematics and Theoretical Computer Science, Volume 36,
American Mathematical Society 1997.
This is a great book!
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ..More.. 
Permutations are re-arrangements of a sequence of items into another order.
For instance, we can permute A,B,C,D into D,B,C,A.
before: ABCD
after : DBCA
Here the D has swopped
places with the A whilst the B and C have not moved.
In general, since we can place A in any of the 4 places, leaving 3 places
for B (4×3=12 ways to place A and B) and so C can go in any of the remaining 2 places
(so D has 1 choice left), then there are 4×3×2 = 24 permutations of 4 objects.
In general, there are n×(n–1)×...×3×2 permutations of n objects.
Suppose we restrict how we may move (permute) each object to
either fix it, leaving it in the same position
or flip it with a neighbour - two items next to each other swop places (they
cannot now be moved again).
However, not all permutations are made of just these two kinds of transformation.
Here are some examples of both kinds permutations on 4 objects: A, B, C and D:
before: ABCD
after : DBCA |  |
This is
not a fix-or-flip permutation since the items flipped, A and D, are not neighbours.
|
before: ABCD
after : BCDA |  |
This is
not a fix-or-flip permutation because although B has switched to where the A was,
A hasn't moved to where the B was.
|
before: ABCD
after : BACD |  |
B and A have flipped and C and D remain
fixed and so this is a fix-or-flip permutation.
|
before: ABCD
after : BADC |  |
A and B are neighbours and have flipped; the same has happened to C and D also.
|
before: ABCD
after : ABCD |  |
Nothing has moved - all 4 items are fixed!
|
For 3 objects, ABC, we have 3x2x1=6 permutations:
| before: | ABC | ABC | ABC | ABC | ABC | ABC |
| after : | ABC | ACB | BAC | BCA | CAB | CBA |
| |  |  |
 |  |
 |  |
Only the first three are fix-or-flip permutations.
In the fourth A has moved more
than 1 place and in the last two C has moved 2 places.
How many fix-or-flip permutations are there for 4 objects? for 5? for n objects? Why?
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ..More.. 
 If you look at a window of one sheet of flat, clear glass, what's on the other side
is quite clear to see. But if you look through the same piece of glass when it is dark
on the other side, for instance into a shop window when the shop is dark,
you can see your own reflection. This time the clear glass is behaving like a mirror.
If you look at a window of one sheet of flat, clear glass, what's on the other side
is quite clear to see. But if you look through the same piece of glass when it is dark
on the other side, for instance into a shop window when the shop is dark,
you can see your own reflection. This time the clear glass is behaving like a mirror.
If you look very closely, you will see that your reflection is actually
doubled - there are two images of your face side by side. This is because your image
is not only reflected off the top surface of the glass but also gets reflected
from the other side of the glass too - which is called
internal reflection.
So a natural question is what happens if we have double glazing
which has two sheets of glass separated by an air gap, that is, 4 reflecting surfaces?
Hang on a minute ... what about three surfaces?? Let's look at that first!
For three surfaces (for example two sheets of glass resting on each other)
what happens depends on whether we are looking through both sheets of glass
(the rays of light come in on one side of the window but exit from the other)
or whether we are looking at our own reflection from the sheets
(the rays of light enter and leave from the same side of the window).
We can ignore the reflection off the top surface - the light bounces off and we get one
reflection. The other cases are the interesting ones - where all the
reflections are internal reflections.
In other words, the light rays must have
actually penetrated the glass and we can get reflections
from one or perhaps both or even none of the two internal surfaces. We
may even get more reflections as the light bounces off the surfaces again and again, some
of the light escaping each time.
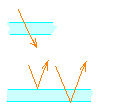
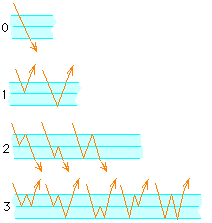 The diagram here shows the possible reflections ordered by the
number of internal reflections,
starting with none (the light goes straight through) to a single internal
reflection (from either of the internal surfaces so there are two cases)
and then exactly two internal reflections and finally we have shown
3 internal reflections.
The diagram here shows the possible reflections ordered by the
number of internal reflections,
starting with none (the light goes straight through) to a single internal
reflection (from either of the internal surfaces so there are two cases)
and then exactly two internal reflections and finally we have shown
3 internal reflections.
If you reflect on this, you'll notice that the Fibonacci numbers seem to
be making themselves clearly visible (groan!). Why?
[Advanced puzzle: What does happen with 4 reflecting surfaces in a double
glazed window?]
 Reflections across Two and Three Glass Plates
by V E Hoggatt Jr and Marjorie Bicknell-Johnson
in The Fibonacci Quarterly, volume 17 (1979), pages 118 - 142.
Reflections across Two and Three Glass Plates
by V E Hoggatt Jr and Marjorie Bicknell-Johnson
in The Fibonacci Quarterly, volume 17 (1979), pages 118 - 142.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ..More.. 
This is a puzzle about puzzles - the puzzle is to design your own puzzle!!
You might have noticed that quite a few of the puzzles above are really "the same"
but the names and situations are changed a bit. It is fairly
easy to see how Leonardo's Leaps
is the same as the 1p and 2p coin change puzzle and also it is
just Leonardo's Lane but slightly disguised.
So...
can you devise your own puzzle where
the answer is the Fibonacci numbers?
The reason the puzzles above are "the same" is that the explanation of
the solution of each of them involves the Fibonacci (recurrence) Rule:
F(n) = F(n–1) + F(n–2)
together with the "initial conditions" that F(0)=0 and F(1)=1
Your puzzle should be based around this relationship.
Do you want to see your name on this page?
Please do email me (see at the foot of this page) with any
new variations that you find. You can then share your idea
with all the other readers of
this page. Let's see how big a collection we can build!
 Here is one puzzle idea to get you thinking. It is about one of my favourite topics -
eating chocolate!
Here is one puzzle idea to get you thinking. It is about one of my favourite topics -
eating chocolate!
Suppose that we need to break a block of chocolate into either just 1 square or a
2-square piece. This makes it similar to the other puzzles above.
Now we need to carefully describe a puzzle that gives the Fibonacci series as the answers.
You may have lots of ideas, but not all of them will give the Fibonacci numbers....
here is one idea that does not give the Fibonacci numbers as its solution:
Suppose we are on a diet but just love chocolate.
So we are allowed either a single square or a 2-square piece -
one or the other but
not both! - and that will be our choice for one day.
How many choice patterns are there if we eat chocolate on 2 days?
Answer:
- We could have 1-square on day 1 and 1-square on day 2,
- or a 2-square piece on day 1 and 1-square on day 2,
- or 1 and then 2
- or even (and here we are desperate!) a 2-square piece on both days.
That gives 4 possibilities over 2 days. But 4 is not a Fibonacci number!
Actually, if we see what could happen over 3 days and 4 and so on, we get an
interesting series
of numbers that you will recognise - but what is it?
How can we change the puzzle so that it does
give the Fibonacci numbers?
In mathematics, when two problems are essentially identical except for names, we call them
isomorphic. This the problem of Steeping Stones and Leonardo's Leap are identical since
we have:
Stones Stairs
jumping stepping
size 1 or 2 size 1 or 2
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ..More.. 
More Links and References
 The
Amazing Mathematical Object Factory has an interesting section on
Fibonacci Numbers
which contains explanations for some of the puzzles on this page and the
relationships between them.
The
Amazing Mathematical Object Factory has an interesting section on
Fibonacci Numbers
which contains explanations for some of the puzzles on this page and the
relationships between them.
References to the maths behind these puzzles
-
Compositions with Ones and Twos
K Alladi, V E Hoggatt Jr Fibonacci Quarterly 13 (1975) pages 233-239
Partitions of n using only 1 and 2
- Zero-One Sequences and Fibonacci Numbers
L Carlitz, R Scoville Fibonacci Quarterly 15 (1977) pages 246-253
Sequences of 0s and 1s with no two consecutive ones
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ..More.. 
 © 1996-2021 Dr Ron Knott
© 1996-2021 Dr Ron Knott


![]()
 There's just one wall pattern which is 1 unit wide - made by putting the brick on its end.
There's just one wall pattern which is 1 unit wide - made by putting the brick on its end.![]()

![]()












 1: step-step-step
1: step-step-step ![]() Applied Combinatorics (4th Edition) by A Tucker, Wiley, 2001, 464 pages.
Applied Combinatorics (4th Edition) by A Tucker, Wiley, 2001, 464 pages.
![]()

![[||]](boxes6.gif)
![[||]](boxes8.gif)
![]() Inspired by
How the odd terms in the Fibonacci Sequence stack up S Rinaldi, D G Rogers, Mathematical Gazette
(2006) pages 431-442 available in
PDF format.
Inspired by
How the odd terms in the Fibonacci Sequence stack up S Rinaldi, D G Rogers, Mathematical Gazette
(2006) pages 431-442 available in
PDF format.




![]() Inspired by
How the odd terms in the Fibonacci Sequence stack up S Rinaldi, D G Rogers, Mathematical Gazette
(2006) pages 431-442.
Inspired by
How the odd terms in the Fibonacci Sequence stack up S Rinaldi, D G Rogers, Mathematical Gazette
(2006) pages 431-442.
![]()
![]() (who cannot be next to each other) and
some are not
(who cannot be next to each other) and
some are not ![]() . The number of seating arrangements is always a Fibonacci number:
. The number of seating arrangements is always a Fibonacci number:![]() are allowed to sit next to each other!
are allowed to sit next to each other!
![]()
![]()
![]()
![]() ...
since the two teachers have the other teacher next to them.
The non-teacher on the right of these 3 will now also need another non-teacher on his other side
so that he too is not left on his own.
...
since the two teachers have the other teacher next to them.
The non-teacher on the right of these 3 will now also need another non-teacher on his other side
so that he too is not left on his own.![]()
![]() See Antisocial Dinner Parties by R Lewis in
Fibonacci Quarterly 1995, vol 33, pages 368-370.
See Antisocial Dinner Parties by R Lewis in
Fibonacci Quarterly 1995, vol 33, pages 368-370.
![]()











![]() Inspired by
Self-avoiding walks and Fibonacci Numbers Arthur T Benjamin Fibonacci Quarterly (2006), pages 330-334.
Inspired by
Self-avoiding walks and Fibonacci Numbers Arthur T Benjamin Fibonacci Quarterly (2006), pages 330-334.
![]()
![]()
![]()
![]() Inspired by Joan Reinthaler's
Discrete Mathematics is Already in the Classroom - But It's Hiding pages 295-299 in:
Inspired by Joan Reinthaler's
Discrete Mathematics is Already in the Classroom - But It's Hiding pages 295-299 in:
![]() Discrete Mathematics in Schools,
DIMACS Series in
Discrete Mathematics and Theoretical Computer Science, Volume 36,
American Mathematical Society 1997.
This is a great book!
Discrete Mathematics in Schools,
DIMACS Series in
Discrete Mathematics and Theoretical Computer Science, Volume 36,
American Mathematical Society 1997.
This is a great book!
![]()
![]()
 If you look at a window of one sheet of flat, clear glass, what's on the other side
is quite clear to see. But if you look through the same piece of glass when it is dark
on the other side, for instance into a shop window when the shop is dark,
you can see your own reflection. This time the clear glass is behaving like a mirror.
If you look at a window of one sheet of flat, clear glass, what's on the other side
is quite clear to see. But if you look through the same piece of glass when it is dark
on the other side, for instance into a shop window when the shop is dark,
you can see your own reflection. This time the clear glass is behaving like a mirror.
 The diagram here shows the possible reflections ordered by the
number of internal reflections,
starting with none (the light goes straight through) to a single internal
reflection (from either of the internal surfaces so there are two cases)
and then exactly two internal reflections and finally we have shown
3 internal reflections.
The diagram here shows the possible reflections ordered by the
number of internal reflections,
starting with none (the light goes straight through) to a single internal
reflection (from either of the internal surfaces so there are two cases)
and then exactly two internal reflections and finally we have shown
3 internal reflections.![]() Reflections across Two and Three Glass Plates
by V E Hoggatt Jr and Marjorie Bicknell-Johnson
in The Fibonacci Quarterly, volume 17 (1979), pages 118 - 142.
Reflections across Two and Three Glass Plates
by V E Hoggatt Jr and Marjorie Bicknell-Johnson
in The Fibonacci Quarterly, volume 17 (1979), pages 118 - 142.
![]()
![]()
![]()